Question
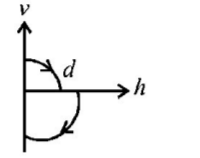
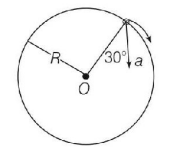
In the given figure, $$a = 15\,m/{s^2}$$ represents the total acceleration of a particle moving in the clockwise direction in a circle of radius $$R = 2.5\,m$$ at a given instant of time. The speed of the particle is
In the given figure, $$a = 15\,m/{s^2}$$ represents the total acceleration of a particle moving in the clockwise direction in a circle of radius $$R = 2.5\,m$$ at a given instant of time. The speed of the particle is
A.
$$4.5\,m/s$$
B.
$$5.0\,m/s$$
C.
$$5.7\,m/s$$
D.
$$6.2\,m/s$$
Answer :
$$5.7\,m/s$$
Solution :
Centripetal acceleration of a particle moving on a circular path is given by $${a_c} = \frac{{{v^2}}}{R}$$
In the given figure,
$$\eqalign{ & {a_c} = a\cos {30^ \circ } = 15\cos {30^ \circ }\,m/{s^2} \cr & \Rightarrow \frac{{{v^2}}}{R} = 15\cos {30^ \circ } \cr & \Rightarrow {v^2} = R \times 15 \times \frac{{\sqrt 3 }}{2} \cr & = 2.5 \times 15 \times \frac{{\sqrt 3 }}{2} \cr & \therefore v = 5.7\,m/s \cr} $$
Centripetal acceleration of a particle moving on a circular path is given by $${a_c} = \frac{{{v^2}}}{R}$$
In the given figure,
$$\eqalign{ & {a_c} = a\cos {30^ \circ } = 15\cos {30^ \circ }\,m/{s^2} \cr & \Rightarrow \frac{{{v^2}}}{R} = 15\cos {30^ \circ } \cr & \Rightarrow {v^2} = R \times 15 \times \frac{{\sqrt 3 }}{2} \cr & = 2.5 \times 15 \times \frac{{\sqrt 3 }}{2} \cr & \therefore v = 5.7\,m/s \cr} $$