Question
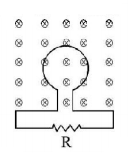
In the figure the flux through the loop perpendicular to the plane of the coil and directed into the paper is varying according to the relation $$\phi = 6{t^2} + 7t + 1$$ where $$\phi $$ is in milliweber and $$t$$ is in second. The magnitude of the emf induced in the loop at $$t = 2\,s$$ and the direction of induce current through $$R$$ are
In the figure the flux through the loop perpendicular to the plane of the coil and directed into the paper is varying according to the relation $$\phi = 6{t^2} + 7t + 1$$ where $$\phi $$ is in milliweber and $$t$$ is in second. The magnitude of the emf induced in the loop at $$t = 2\,s$$ and the direction of induce current through $$R$$ are
A.
$$39\,mV;$$ right to left
B.
$$39\,mV;$$ left to right
C.
$$31\,mV;$$ right to left
D.
$$31\,mV;$$ left to right
Answer :
$$39\,mV;$$ right to left
Solution :
$$\eqalign{ & \phi = 6{t^2} + 7t + 1 \cr & \Rightarrow \frac{{d\phi }}{{dt}} = 12t + 7 \cr} $$
At time, $$t = 2\,\sec.$$
$$\frac{{d\phi }}{{dt}} = 24 + 7 = 31\,mv$$
Direction of current is from left to right according to Flemings right hand rule.
$$\eqalign{ & \phi = 6{t^2} + 7t + 1 \cr & \Rightarrow \frac{{d\phi }}{{dt}} = 12t + 7 \cr} $$
At time, $$t = 2\,\sec.$$
$$\frac{{d\phi }}{{dt}} = 24 + 7 = 31\,mv$$
Direction of current is from left to right according to Flemings right hand rule.
