Question
In older times, people used to think that the earth was flat. Imagine that the earth is indeed not a sphere of radius $$R,$$ but an infinite plate of thickness $$H.$$ What value of $$H$$ is needed to allow the same gravitational acceleration to be experienced as on the surface of the actual earth? (Assume that the earth’s density is uniform and equal in the two models)
A.
$$\frac{{2R}}{3}$$
B.
$$\frac{{4R}}{3}$$
C.
$$\frac{{8R}}{3}$$
D.
$$\frac{{R}}{3}$$
Answer :
$$\frac{{2R}}{3}$$
Solution :
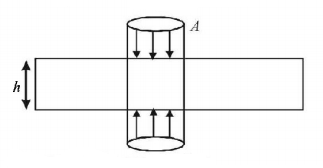
Gauss law for gravitation
$$\eqalign{ & \int {\vec g \cdot d\vec s = - {m_{{\text{in}}}} \cdot 4\pi G;g = \frac{{GM}}{{{R^2}}}} \cr & 2 \times \frac{{GM}}{{{R^2}}} \times A = \frac{M}{{\frac{4}{3}\pi {R^3}}}\left( {h \times A} \right) \times 4\pi G \cr & \Rightarrow h = \frac{{2R}}{3} \cr} $$

Gauss law for gravitation
$$\eqalign{ & \int {\vec g \cdot d\vec s = - {m_{{\text{in}}}} \cdot 4\pi G;g = \frac{{GM}}{{{R^2}}}} \cr & 2 \times \frac{{GM}}{{{R^2}}} \times A = \frac{M}{{\frac{4}{3}\pi {R^3}}}\left( {h \times A} \right) \times 4\pi G \cr & \Rightarrow h = \frac{{2R}}{3} \cr} $$