Question
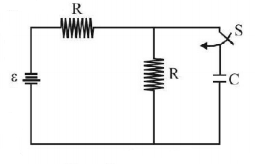
In given circuit capacitor initially uncharged. Now at $$t = 0$$ switch $$S$$ is closed then current given by source at any time $$t$$ is
In given circuit capacitor initially uncharged. Now at $$t = 0$$ switch $$S$$ is closed then current given by source at any time $$t$$ is
A.
$$\frac{2}{R}\left( {1 - {e^{\frac{{ - 2t}}{{CR}}}}} \right)$$
B.
$$\frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - 2t}}{{CR}}}}} \right)$$
C.
$$\frac{\varepsilon }{{2R}}\left( {1 - {e^{\frac{{ - 2t}}{{CR}}}}} \right)$$
D.
$$\frac{{2\varepsilon }}{R}\left( {1 - {e^{\frac{{ - 2t}}{{CR}}}}} \right)$$
Answer :
$$\frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - 2t}}{{CR}}}}} \right)$$
Solution :
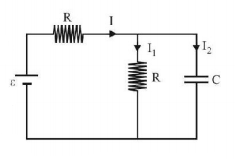
$$\eqalign{ & Q = \frac{{EC}}{2}\left( {1 - {e^{\frac{{ - t}}{\tau }}}} \right) \cr & {I_2} = \frac{{\varepsilon C}}{{2r}}{e^{\frac{{ - t}}{\tau }}} = \frac{\varepsilon }{R}{e^{\frac{{ - t}}{\tau }}} \cr & {I_1} = \frac{{Vc}}{R} = \frac{{\frac{\varepsilon }{2}}}{R}\left( {1 - {e^{\frac{{ - t}}{\tau }}}} \right) \cr & {I_1} = \frac{\varepsilon }{R} - {e^{\frac{{ - t}}{\tau }}} + \frac{\varepsilon }{{2R}} - \frac{\varepsilon }{{2R}}{\varepsilon ^{\frac{{ - t}}{\tau }}} \cr & \frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - t}}{\tau }}}} \right) = \frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - 2t}}{{CR}}}}} \right) \cr} $$

$$\eqalign{ & Q = \frac{{EC}}{2}\left( {1 - {e^{\frac{{ - t}}{\tau }}}} \right) \cr & {I_2} = \frac{{\varepsilon C}}{{2r}}{e^{\frac{{ - t}}{\tau }}} = \frac{\varepsilon }{R}{e^{\frac{{ - t}}{\tau }}} \cr & {I_1} = \frac{{Vc}}{R} = \frac{{\frac{\varepsilon }{2}}}{R}\left( {1 - {e^{\frac{{ - t}}{\tau }}}} \right) \cr & {I_1} = \frac{\varepsilon }{R} - {e^{\frac{{ - t}}{\tau }}} + \frac{\varepsilon }{{2R}} - \frac{\varepsilon }{{2R}}{\varepsilon ^{\frac{{ - t}}{\tau }}} \cr & \frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - t}}{\tau }}}} \right) = \frac{\varepsilon }{{2R}}\left( {1 + {e^{\frac{{ - 2t}}{{CR}}}}} \right) \cr} $$