Question
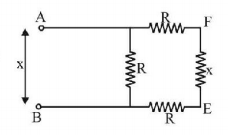
In Fig. find the value of resistor to be connected between $$C$$ and $$D,$$ so that the resistance of the entire circuit between $$A$$ and $$B$$ does not change with the number of elementary sets.
In Fig. find the value of resistor to be connected between $$C$$ and $$D,$$ so that the resistance of the entire circuit between $$A$$ and $$B$$ does not change with the number of elementary sets.

A.
$$R$$
B.
$$R\left( {\sqrt 3 - 1} \right)$$
C.
$$3\,R$$
D.
$$R\left( {\sqrt 3 + 1} \right)$$
Answer :
$$R\left( {\sqrt 3 - 1} \right)$$
Solution :
Let the resistor to be connected across $$CD$$ be $$x.$$ Then the equivalent resistance across $$EF$$ should be $$x$$ and also across $$AB$$ should be $$x.$$ So we get
$$\frac{{\left( {2R + x} \right)R}}{{3R + x}} = x$$
solve to get
$$x = \left( {\sqrt 3 - 1} \right)R$$
Let the resistor to be connected across $$CD$$ be $$x.$$ Then the equivalent resistance across $$EF$$ should be $$x$$ and also across $$AB$$ should be $$x.$$ So we get
$$\frac{{\left( {2R + x} \right)R}}{{3R + x}} = x$$

solve to get
$$x = \left( {\sqrt 3 - 1} \right)R$$