Question
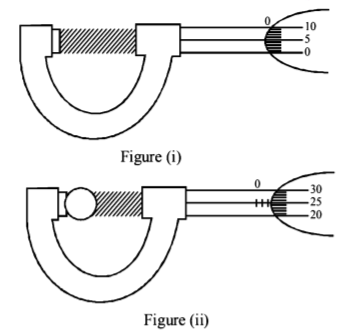
In a screw gauge, the zero of mainscale coincides with fifth division of circular scale in figure $$\left( {\text{i}} \right)$$. The circular division of screw gauge are $$50.$$ It moves $$0.5 \,mm$$ on main scale in one rotation. The diameter of the ball in figure $$\left( {\text{ii}} \right)$$ is-
In a screw gauge, the zero of mainscale coincides with fifth division of circular scale in figure $$\left( {\text{i}} \right)$$. The circular division of screw gauge are $$50.$$ It moves $$0.5 \,mm$$ on main scale in one rotation. The diameter of the ball in figure $$\left( {\text{ii}} \right)$$ is-
A.
2.25 $$mm$$
B.
2.20 $$mm$$
C.
1.20 $$mm$$
D.
1.25 $$mm$$
Answer :
1.20 $$mm$$
Solution :
Least count $$ = \frac{{0.5}}{{50}} = 0.01\,mm$$
Zero error = 5 $$× L.C. = 5 × 0.01\,mm = 0.05\,mm$$
Diameter of ball = [Reading on main scale] + [Reading on circular scale $$× L.C.$$ ] $$-$$ Zero error
= 0.5 × 2 + 25 × 0.01 $$-$$ 0.05
= 1.20 $$mm$$
Least count $$ = \frac{{0.5}}{{50}} = 0.01\,mm$$
Zero error = 5 $$× L.C. = 5 × 0.01\,mm = 0.05\,mm$$
Diameter of ball = [Reading on main scale] + [Reading on circular scale $$× L.C.$$ ] $$-$$ Zero error
= 0.5 × 2 + 25 × 0.01 $$-$$ 0.05
= 1.20 $$mm$$