Question
If $$g$$ is the acceleration due to gravity on the earth’s surface, the gain in the potential energy of an object of mass $$m$$ raised from the surface of the earth to a height equal to the radius $$R$$ of the earth, is-
A.
$$\frac{1}{2}\,mgR$$
B.
$$2\,mgR$$
C.
$$mgR$$
D.
$$\frac{1}{4}mgR$$
Answer :
$$\frac{1}{2}\,mgR$$
Solution :
$${U_i} = - \frac{{GMm}}{R} = $$ Initial potential energy of the system.
$${U_f} = - \frac{{GMm}}{{2R}} = $$ Final P.E. of the system.
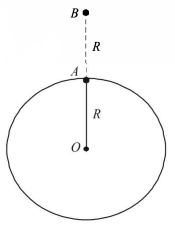
$$\eqalign{ & \therefore \Delta U = {U_f} - {U_i} \cr & = - GMm\left[ {\frac{1}{{2R}} - \frac{1}{R}} \right] = \frac{{GMm}}{{2R}}\,.....(i) \cr & {\text{But }}g = \frac{{GM}}{{{R^2}}} \cr & \therefore GM = g{R^2}\,.....(ii) \cr & {\text{From (i) and (ii)}} \cr & \Delta U = \frac{{g{R^2}m}}{{2R}} = \frac{{mgR}}{2} \cr} $$
$${U_i} = - \frac{{GMm}}{R} = $$ Initial potential energy of the system.
$${U_f} = - \frac{{GMm}}{{2R}} = $$ Final P.E. of the system.

$$\eqalign{ & \therefore \Delta U = {U_f} - {U_i} \cr & = - GMm\left[ {\frac{1}{{2R}} - \frac{1}{R}} \right] = \frac{{GMm}}{{2R}}\,.....(i) \cr & {\text{But }}g = \frac{{GM}}{{{R^2}}} \cr & \therefore GM = g{R^2}\,.....(ii) \cr & {\text{From (i) and (ii)}} \cr & \Delta U = \frac{{g{R^2}m}}{{2R}} = \frac{{mgR}}{2} \cr} $$