Question
If a steady current $$I$$ is flowing through a cylindrical element $$ABC.$$ Choose the correct relationship
If a steady current $$I$$ is flowing through a cylindrical element $$ABC.$$ Choose the correct relationship
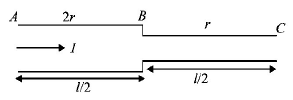
A.
$${V_{AB}} = 2{V_{BC}}$$
B.
Power across $$BC$$ is 4 times the power across $$AB$$
C.
Current densities in $$AB$$ and $$BC$$ are equal
D.
Electric field due to current inside $$AB$$ and $$BC$$ are equal
Answer :
Power across $$BC$$ is 4 times the power across $$AB$$
Solution :
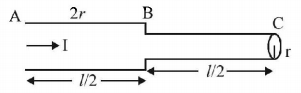
$$\left( A \right)\,\frac{{{V_{AB}}}}{{{V_{BC}}}} = \frac{{{I_{AB}}{R_{AB}}}}{{{I_{BC}}{R_{BC}}}} = \frac{{{R_{AB}}}}{{{R_{BC}}}} = \frac{{\rho \frac{\ell }{{2\left[ {\pi \times 4{r^2}} \right]}}}}{{\rho \frac{\ell }{{2\left[ {\pi {r^2}} \right]}}}} = \frac{1}{4}$$
$$\left[ {{I_{AB}} = {I_{BC}},\,{\text{wire is of same material}}} \right]$$
Therefore option (A) is incorrect.
$$\left( B \right)\,\frac{{{P_{BC}}}}{{{P_{AB}}}} = \frac{{{I^2}{R_{BC}}}}{{{I^2}{R_{AB}}}} = \frac{{\rho \frac{\ell }{{2\left[ {\pi \times 4{r^2}} \right]}}}}{{\rho \frac{\ell }{{2\left[ {\pi {r^2}} \right]}}}} = \frac{1}{4}$$
$$\therefore {P_{AB}} = 4{P_{BC}};$$ Therefore (B) is correct.
$$\left( C \right)\,\frac{{{J_{AB}}}}{{{J_{BC}}}} = \frac{{\frac{I}{{\pi \times 4{r^2}}}}}{{\frac{I}{{\pi \times {r^2}}}}} = \frac{1}{4};$$ Therefore (C) is incorrect.
$$\left( D \right)\,\frac{{{E_{AB}}}}{{{E_{BC}}}} = \frac{{\left[ {\frac{{{V_{AB}}}}{{\frac{\ell }{2}}}} \right]}}{{\left[ {\frac{{{V_{BC}}}}{{\frac{\ell }{2}}}} \right]}} = \frac{1}{4};$$ Therefore (D) is incorrect.

$$\left( A \right)\,\frac{{{V_{AB}}}}{{{V_{BC}}}} = \frac{{{I_{AB}}{R_{AB}}}}{{{I_{BC}}{R_{BC}}}} = \frac{{{R_{AB}}}}{{{R_{BC}}}} = \frac{{\rho \frac{\ell }{{2\left[ {\pi \times 4{r^2}} \right]}}}}{{\rho \frac{\ell }{{2\left[ {\pi {r^2}} \right]}}}} = \frac{1}{4}$$
$$\left[ {{I_{AB}} = {I_{BC}},\,{\text{wire is of same material}}} \right]$$
Therefore option (A) is incorrect.
$$\left( B \right)\,\frac{{{P_{BC}}}}{{{P_{AB}}}} = \frac{{{I^2}{R_{BC}}}}{{{I^2}{R_{AB}}}} = \frac{{\rho \frac{\ell }{{2\left[ {\pi \times 4{r^2}} \right]}}}}{{\rho \frac{\ell }{{2\left[ {\pi {r^2}} \right]}}}} = \frac{1}{4}$$
$$\therefore {P_{AB}} = 4{P_{BC}};$$ Therefore (B) is correct.
$$\left( C \right)\,\frac{{{J_{AB}}}}{{{J_{BC}}}} = \frac{{\frac{I}{{\pi \times 4{r^2}}}}}{{\frac{I}{{\pi \times {r^2}}}}} = \frac{1}{4};$$ Therefore (C) is incorrect.
$$\left( D \right)\,\frac{{{E_{AB}}}}{{{E_{BC}}}} = \frac{{\left[ {\frac{{{V_{AB}}}}{{\frac{\ell }{2}}}} \right]}}{{\left[ {\frac{{{V_{BC}}}}{{\frac{\ell }{2}}}} \right]}} = \frac{1}{4};$$ Therefore (D) is incorrect.