Question
If a ball is thrown vertically upwards with speed $$u,$$ the distance covered during the last $$t$$ $$\sec$$ of its ascent is
A.
$$ut - \frac{1}{2}g{t^2}$$
B.
$$\left( {u + gt} \right)t$$
C.
$$ut$$
D.
$$\frac{1}{2}g{t^2}$$
Answer :
$$\frac{1}{2}g{t^2}$$
Solution :
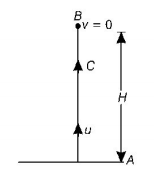
Let the ball takes $$T$$ second to reach maximum height $$H.$$
$$v = u - gT$$
put $$v = 0$$ (at height $$H$$ )
$$\eqalign{ & \therefore u = gT \cr & {\text{or}}\,T = \frac{u}{g}\,......\left( {\text{i}} \right) \cr} $$
Velocity attained by the ball in $$\left( {T - t} \right)s$$ is,
$$\eqalign{ & v' = u - g\left( {T - t} \right) = u - gT + gt \cr & = u - g\frac{u}{g} + gt = u - u + gt \cr & v' = gt\,.......\left( {{\text{ii}}} \right) \cr} $$
Hence, distance travelled in last $$t\,\sec$$ of its ascent
$$\eqalign{ & CB = v't - \frac{1}{2}g{t^2} = \left( {gt} \right)t - \frac{1}{2}g{t^2} \cr & = g{t^2} - \frac{1}{2}g{t^2}\,\,\left[ {{\text{From}}\,{\text{Eq}}{\text{.}}\,\left( {{\text{ii}}} \right)} \right] \cr & = \frac{1}{2}g{t^2} \cr} $$

Let the ball takes $$T$$ second to reach maximum height $$H.$$
$$v = u - gT$$
put $$v = 0$$ (at height $$H$$ )
$$\eqalign{ & \therefore u = gT \cr & {\text{or}}\,T = \frac{u}{g}\,......\left( {\text{i}} \right) \cr} $$
Velocity attained by the ball in $$\left( {T - t} \right)s$$ is,
$$\eqalign{ & v' = u - g\left( {T - t} \right) = u - gT + gt \cr & = u - g\frac{u}{g} + gt = u - u + gt \cr & v' = gt\,.......\left( {{\text{ii}}} \right) \cr} $$
Hence, distance travelled in last $$t\,\sec$$ of its ascent
$$\eqalign{ & CB = v't - \frac{1}{2}g{t^2} = \left( {gt} \right)t - \frac{1}{2}g{t^2} \cr & = g{t^2} - \frac{1}{2}g{t^2}\,\,\left[ {{\text{From}}\,{\text{Eq}}{\text{.}}\,\left( {{\text{ii}}} \right)} \right] \cr & = \frac{1}{2}g{t^2} \cr} $$