Question
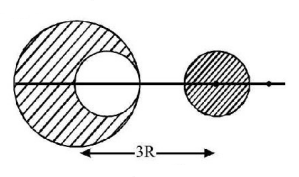
From a sphere of mass $$M$$ and radius $$R,$$ a smaller sphere of radius $$\frac{R}{2}$$ is carved out such that the cavity made in the original sphere is between its centre and the periphery (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is $$3R,$$ the gravitational force between the two sphere is
From a sphere of mass $$M$$ and radius $$R,$$ a smaller sphere of radius $$\frac{R}{2}$$ is carved out such that the cavity made in the original sphere is between its centre and the periphery (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is $$3R,$$ the gravitational force between the two sphere is
A.
$$\frac{{41\,G{M^2}}}{{3600\,{R^2}}}$$
B.
$$\frac{{41\,G{M^2}}}{{450\,{R^2}}}$$
C.
$$\frac{{59\,G{M^2}}}{{450\,{R^2}}}$$
D.
$$\frac{{G{M^2}}}{{225\,{R^2}}}$$
Answer :
$$\frac{{41\,G{M^2}}}{{3600\,{R^2}}}$$
Solution :
Volume of removed sphere
$${V_{{\text{remo}}}} = \frac{4}{3}\pi {\left( {\frac{R}{2}} \right)^3} = \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right)$$
Volume of the sphere (remaining)
$${V_{{\text{remain}}}} = \frac{4}{3}\pi {R^3} - \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right) = \frac{4}{3}\pi {R^3}\left( {\frac{7}{8}} \right)$$
Therefore mass of sphere carved and remaining sphere are at respectively $$\frac{1}{8}M$$ and $$\frac{7}{8}M.$$
Therefore, gravitational force between these two sphere,
$$\eqalign{ & F = \frac{{GMm}}{{{r^2}}} = \frac{{G\frac{{7M}}{8} \times \frac{1}{8}M}}{{{{\left( {3R} \right)}^2}}} = \frac{7}{{64 \times 9}}\frac{{G{M^2}}}{{{R^2}}} \cr & \simeq \frac{{41}}{{3600}}\frac{{G{M^2}}}{{{R^2}}} \cr} $$
Volume of removed sphere
$${V_{{\text{remo}}}} = \frac{4}{3}\pi {\left( {\frac{R}{2}} \right)^3} = \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right)$$
Volume of the sphere (remaining)
$${V_{{\text{remain}}}} = \frac{4}{3}\pi {R^3} - \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right) = \frac{4}{3}\pi {R^3}\left( {\frac{7}{8}} \right)$$
Therefore mass of sphere carved and remaining sphere are at respectively $$\frac{1}{8}M$$ and $$\frac{7}{8}M.$$
Therefore, gravitational force between these two sphere,
$$\eqalign{ & F = \frac{{GMm}}{{{r^2}}} = \frac{{G\frac{{7M}}{8} \times \frac{1}{8}M}}{{{{\left( {3R} \right)}^2}}} = \frac{7}{{64 \times 9}}\frac{{G{M^2}}}{{{R^2}}} \cr & \simeq \frac{{41}}{{3600}}\frac{{G{M^2}}}{{{R^2}}} \cr} $$