Question
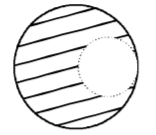
From a solid sphere of mass $$M$$ and radius $$R,$$ a spherical portion of radius $$\frac{R}{2}$$ is removed, as shown in the figure. Taking gravitational potential $$V=0$$ at $$r = \infty ,$$ the potential at the centre of the cavity thus formed is-
From a solid sphere of mass $$M$$ and radius $$R,$$ a spherical portion of radius $$\frac{R}{2}$$ is removed, as shown in the figure. Taking gravitational potential $$V=0$$ at $$r = \infty ,$$ the potential at the centre of the cavity thus formed is-
($$G\,=$$ gravitational constant)
A.
$$\frac{{ - 2GM}}{{3R}}$$
B.
$$\frac{{ - 2GM}}{{R}}$$
C.
$$\frac{{ - GM}}{{2R}}$$
D.
$$\frac{{ - GM}}{{R}}$$
Answer :
$$\frac{{ - GM}}{{R}}$$
Solution :
Due to complete solid sphere, potential at point $$P$$
$$\eqalign{ & {V_{sphere}} = \frac{{ - GM}}{{2{R^3}}}\left[ {3{R^2} - {{\left( {\frac{R}{2}} \right)}^2}} \right] \cr & = \frac{{ - GM}}{{2{R^3}}}\left( {\frac{{11{R^2}}}{4}} \right) \cr & = - 11\frac{{GM}}{{8R}} \cr} $$
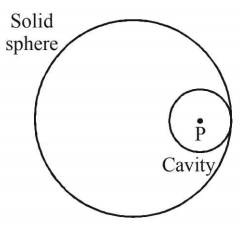
Due to cavity part potential at point P
$${V_{cavity}} = - \frac{3}{2}\frac{{\frac{{GM}}{8}}}{{\frac{R}{2}}} = - \frac{{3GM}}{{8R}}$$
So potential at the centre of cavity
$$ = {V_{sphere}} - {V_{cavity}} = - \frac{{11GM}}{{8R}} - \left( { - \frac{3}{8}\frac{{GM}}{R}} \right) = \frac{{ - GM}}{R}$$
Due to complete solid sphere, potential at point $$P$$
$$\eqalign{ & {V_{sphere}} = \frac{{ - GM}}{{2{R^3}}}\left[ {3{R^2} - {{\left( {\frac{R}{2}} \right)}^2}} \right] \cr & = \frac{{ - GM}}{{2{R^3}}}\left( {\frac{{11{R^2}}}{4}} \right) \cr & = - 11\frac{{GM}}{{8R}} \cr} $$

Due to cavity part potential at point P
$${V_{cavity}} = - \frac{3}{2}\frac{{\frac{{GM}}{8}}}{{\frac{R}{2}}} = - \frac{{3GM}}{{8R}}$$
So potential at the centre of cavity
$$ = {V_{sphere}} - {V_{cavity}} = - \frac{{11GM}}{{8R}} - \left( { - \frac{3}{8}\frac{{GM}}{R}} \right) = \frac{{ - GM}}{R}$$