Question
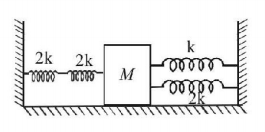
Four massless springs whose force constants are $$2k, 2k, k$$ and $$2k$$ respectively are attached to a mass $$M$$ kept on a frictionless plane (as shown in figure). If the mass $$M$$ is displaced in the horizontal direction, then the frequency of the system is
Four massless springs whose force constants are $$2k, 2k, k$$ and $$2k$$ respectively are attached to a mass $$M$$ kept on a frictionless plane (as shown in figure). If the mass $$M$$ is displaced in the horizontal direction, then the frequency of the system is
A.
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{{4M}}} $$
B.
$$\frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$
C.
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{{7M}}} $$
D.
$$\frac{1}{{2\pi }}\sqrt {\frac{{7k}}{M}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$
Solution :
Springs on the left of the block are in series, hence their equivalent spring constant is
$${K_1} = \frac{{\left( {2k} \right)\left( {2k} \right)}}{{2k + 2k}} = k$$
Springs on the right of the block are in parallel, hence their equivalent spring constant is
$${k_2} = k + 2k = 3k$$
Now again both $${K_1}$$ and $${K_2}$$ are in parallel
$$\therefore {K_{{\text{eq}}}} = {k_1} + {k_2} = k + 3k = 4k$$
Hence, frequency is
$$f = \frac{1}{{2\pi }}\sqrt {\frac{{{K_{{\text{eq}}}}}}{M}} = \frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$
Springs on the left of the block are in series, hence their equivalent spring constant is
$${K_1} = \frac{{\left( {2k} \right)\left( {2k} \right)}}{{2k + 2k}} = k$$
Springs on the right of the block are in parallel, hence their equivalent spring constant is
$${k_2} = k + 2k = 3k$$
Now again both $${K_1}$$ and $${K_2}$$ are in parallel
$$\therefore {K_{{\text{eq}}}} = {k_1} + {k_2} = k + 3k = 4k$$
Hence, frequency is
$$f = \frac{1}{{2\pi }}\sqrt {\frac{{{K_{{\text{eq}}}}}}{M}} = \frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$