Question
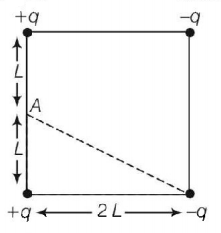
Four electric charges $$ + q, + q, - q$$ and $$- q$$ are placed at the corners of a square of side $$2L$$ (see figure). The electric potential at point $$A,$$ mid-way between the two charges $$+q$$ and $$+q$$ is
Four electric charges $$ + q, + q, - q$$ and $$- q$$ are placed at the corners of a square of side $$2L$$ (see figure). The electric potential at point $$A,$$ mid-way between the two charges $$+q$$ and $$+q$$ is
A.
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 + \frac{1}{{\sqrt 5 }}} \right)$$
B.
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)$$
C.
zero
D.
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 + \sqrt 5 } \right)$$
Answer :
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)$$
Solution :
Potential at any distance $$r$$ due to a point charge is given by,
$$V = \frac{{kq}}{r}\,\,\left[ {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right]$$
Given, $$V = 2{V_{{\text{positive}}}} + 2{V_{{\text{negative}}}}$$
$$\eqalign{ & = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{2q}}{L} - \frac{{2q}}{{L\sqrt 5 }}} \right] \cr & V = \frac{{2q}}{{4\pi {\varepsilon _0}L}}\left( {1 - \frac{1}{{\sqrt 5 }}} \right) \cr} $$
Potential at any distance $$r$$ due to a point charge is given by,
$$V = \frac{{kq}}{r}\,\,\left[ {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right]$$
Given, $$V = 2{V_{{\text{positive}}}} + 2{V_{{\text{negative}}}}$$
$$\eqalign{ & = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{2q}}{L} - \frac{{2q}}{{L\sqrt 5 }}} \right] \cr & V = \frac{{2q}}{{4\pi {\varepsilon _0}L}}\left( {1 - \frac{1}{{\sqrt 5 }}} \right) \cr} $$