Question
Following figure shows two processes $$A$$ and $$B$$ for a gas. If $$\Delta {Q_A}$$ and $$\Delta {Q_B}$$ are the amount of heat absorbed by the system in two cases, and $$\Delta {U_A}$$ and $$\Delta {U_B}$$ are changes in internal energies, respectively, then :
Following figure shows two processes $$A$$ and $$B$$ for a gas. If $$\Delta {Q_A}$$ and $$\Delta {Q_B}$$ are the amount of heat absorbed by the system in two cases, and $$\Delta {U_A}$$ and $$\Delta {U_B}$$ are changes in internal energies, respectively, then :
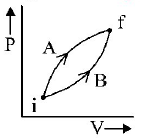
A.
$$\Delta {Q_A} < \Delta {Q_B},\Delta {U_A} < \Delta {U_B}$$
B.
$$\Delta {Q_A} > \Delta {Q_B},\Delta {U_A} > \Delta {U_B}$$
C.
$$\Delta {Q_A} > \Delta {Q_B},\Delta {U_A} = \Delta {U_B}$$
D.
$$\Delta {Q_A} = \Delta {Q_B},\Delta {U_A} = \Delta {U_B}$$
Answer :
$$\Delta {Q_A} > \Delta {Q_B},\Delta {U_A} = \Delta {U_B}$$
Solution :
Internal energy depends only on initial and final state
So, $$\Delta {U_A} = \Delta {U_B}$$
$$\eqalign{ & {\text{Also }}\Delta Q = \Delta U + \Delta W \cr & \therefore \,\,{W_A} > {W_B} \cr & \Rightarrow \,\,\Delta {Q_A} > \Delta {Q_B} \cr} $$
[Area under $$P - V$$ ; graph gives the work done. ]
Internal energy depends only on initial and final state
So, $$\Delta {U_A} = \Delta {U_B}$$
$$\eqalign{ & {\text{Also }}\Delta Q = \Delta U + \Delta W \cr & \therefore \,\,{W_A} > {W_B} \cr & \Rightarrow \,\,\Delta {Q_A} > \Delta {Q_B} \cr} $$
[Area under $$P - V$$ ; graph gives the work done. ]