Question
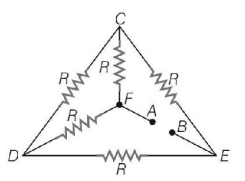
Five equal resistances each of resistance $$R$$ are connected as shown in the figure. A battery of $$4\,V$$ volts is connected between $$A$$ and $$B.$$ The current flowing in $$AFCEB$$ will be
Five equal resistances each of resistance $$R$$ are connected as shown in the figure. A battery of $$4\,V$$ volts is connected between $$A$$ and $$B.$$ The current flowing in $$AFCEB$$ will be
A.
$$\frac{{3V}}{R}$$
B.
$$\frac{V}{R}$$
C.
$$\frac{V}{{2R}}$$
D.
$$\frac{{2V}}{R}$$
Answer :
$$\frac{V}{{2R}}$$
Solution :
The given circuit can be redrawn as shown.
From circuit, $$\frac{{FC}}{{CE}} = \frac{{FD}}{{DE}} = 1$$
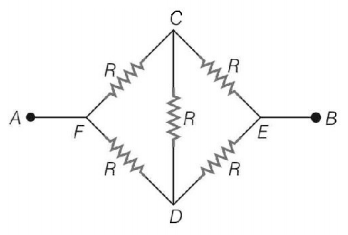
Thus, it is balanced Wheatstone bridge, so, resistance in arm $$CD$$ is ineffective and so no current flows in this arm.
Net resistance of the circuit is
$$\eqalign{ & \frac{1}{{R'}} = \frac{1}{{\left( {R + R} \right)}} + \frac{1}{{\left( {R + R} \right)}} \cr & = \frac{1}{{2R}} + \frac{1}{{2R}} = \frac{2}{{2R}} = \frac{1}{R} \cr & \therefore R' = R \cr} $$
So, net current drawn from the battery is
$$i' = \frac{V}{{R'}} = \frac{V}{R}$$
As from symmetry, upper circuit $$AFCEB$$ is half of the whole circuit and is equal to $$AFDEB.$$ So, in both the halves half of the total current will flow.
Hence, in $$AFCEB,$$ the current flowing is
$$i = \frac{{i'}}{2} = \frac{V}{{2R}}$$
The given circuit can be redrawn as shown.
From circuit, $$\frac{{FC}}{{CE}} = \frac{{FD}}{{DE}} = 1$$

Thus, it is balanced Wheatstone bridge, so, resistance in arm $$CD$$ is ineffective and so no current flows in this arm.
Net resistance of the circuit is
$$\eqalign{ & \frac{1}{{R'}} = \frac{1}{{\left( {R + R} \right)}} + \frac{1}{{\left( {R + R} \right)}} \cr & = \frac{1}{{2R}} + \frac{1}{{2R}} = \frac{2}{{2R}} = \frac{1}{R} \cr & \therefore R' = R \cr} $$
So, net current drawn from the battery is
$$i' = \frac{V}{{R'}} = \frac{V}{R}$$
As from symmetry, upper circuit $$AFCEB$$ is half of the whole circuit and is equal to $$AFDEB.$$ So, in both the halves half of the total current will flow.
Hence, in $$AFCEB,$$ the current flowing is
$$i = \frac{{i'}}{2} = \frac{V}{{2R}}$$