Question
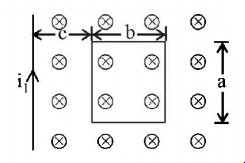
Figure shows a rectangular coil near a long wire. The mutual inductance of the combination is
Figure shows a rectangular coil near a long wire. The mutual inductance of the combination is
A.
$$\frac{{{\mu _0}a}}{{2\pi }}\ln \left( {1 - \frac{b}{c}} \right)$$
B.
$$\frac{{{\mu _0}a}}{{2\pi }}\ln \left( {1 + \frac{b}{c}} \right)$$
C.
$$\frac{{{\mu _0}a}}{\pi }\ln \left( {1 + \frac{b}{c}} \right)$$
D.
$$\frac{{{\mu _0}a}}{{\sqrt 2 \pi }}\ln \left( {1 + \frac{b}{c}} \right)$$
Answer :
$$\frac{{{\mu _0}a}}{{2\pi }}\ln \left( {1 + \frac{b}{c}} \right)$$
Solution :
Let current $${i_1}$$ in straight wire be upward. Then the magnetic field due to the straight wire has magnitude $${B_1} = \frac{{{\mu _0}{i_1}}}{{2\pi r}}$$ at distance $$r.$$ In accrodance with right hand rule, $${B_1}$$ points inward to the plane of page. We consider a differential strip of thickness $$dr,$$ area $$d{A_2} = a\,dr.$$ Magnetic flux through area $$dA,d{\phi _B} = {B_1}\left( {a\,dr} \right).$$
Total flux through the loop,
$$\eqalign{ & {\phi _B} = \int {{B_1}adr = } \int_c^{c + b} {\frac{{{\mu _0}{i_1}}}{{2\pi r}}} a\,dr \cr & = \frac{{{\mu _0}{i_1}a}}{{2\pi }}\int_c^{c + b} {\frac{{dr}}{r}} = \frac{{{\mu _0}{i_1}a}}{{2\pi }}\ln \left( {\frac{{c + b}}{c}} \right) \cr} $$
Therefore mutual inductance,
$$M = \frac{\phi }{{{i_1}}} = \frac{{{\mu _0}a}}{{2\pi }}\ln \left( {1 + \frac{b}{c}} \right)$$
Let current $${i_1}$$ in straight wire be upward. Then the magnetic field due to the straight wire has magnitude $${B_1} = \frac{{{\mu _0}{i_1}}}{{2\pi r}}$$ at distance $$r.$$ In accrodance with right hand rule, $${B_1}$$ points inward to the plane of page. We consider a differential strip of thickness $$dr,$$ area $$d{A_2} = a\,dr.$$ Magnetic flux through area $$dA,d{\phi _B} = {B_1}\left( {a\,dr} \right).$$
Total flux through the loop,
$$\eqalign{ & {\phi _B} = \int {{B_1}adr = } \int_c^{c + b} {\frac{{{\mu _0}{i_1}}}{{2\pi r}}} a\,dr \cr & = \frac{{{\mu _0}{i_1}a}}{{2\pi }}\int_c^{c + b} {\frac{{dr}}{r}} = \frac{{{\mu _0}{i_1}a}}{{2\pi }}\ln \left( {\frac{{c + b}}{c}} \right) \cr} $$
Therefore mutual inductance,
$$M = \frac{\phi }{{{i_1}}} = \frac{{{\mu _0}a}}{{2\pi }}\ln \left( {1 + \frac{b}{c}} \right)$$
