Question
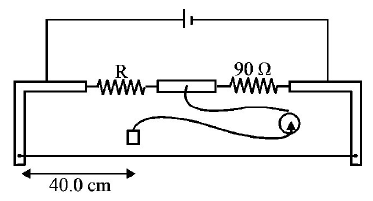
During an experiment with a metre bridge, the galvanometer shows a null point when the jockey is pressed at $$40.0\,cm$$ using a standard resistance of $$90\,\Omega ,$$ as shown in the figure. The least count of the scale used in the metre bridge is $$1mm.$$ The unknown resistance is
During an experiment with a metre bridge, the galvanometer shows a null point when the jockey is pressed at $$40.0\,cm$$ using a standard resistance of $$90\,\Omega ,$$ as shown in the figure. The least count of the scale used in the metre bridge is $$1mm.$$ The unknown resistance is
A.
$$60 \pm 0.15\,\Omega $$
B.
$$135 \pm 0.56\,\Omega $$
C.
$$60 \pm 0.25\,\Omega $$
D.
$$135 \pm 0.23\,\Omega $$
Answer :
$$60 \pm 0.25\,\Omega $$
Solution :
In case of a meter bridge
$$\eqalign{ & \frac{R}{l} = \frac{X}{{100 - l}}\,{\text{Here}}\,X = 90\Omega ,l = 40.0\;cm \cr & \therefore R = \frac{{Xl}}{{100 - l}} \cr} $$
For finding the value of $$R$$
$$R = \frac{{90 \times 40}}{{60}} = 60\Omega $$
For finding the value of $$\Delta R$$
$$\eqalign{ & \frac{{\Delta R}}{R} = \frac{{\Delta l}}{l} + \frac{{\Delta \left( {100 - l} \right)}}{{100 - l}} \cr & \therefore \frac{{\Delta R}}{{60}} = \frac{{0.1}}{{40}} + \frac{{0.1}}{{60}} \cr & \therefore \Delta R = 0.25\Omega \cr} $$
Therefore, $$R = \left( {60 \pm 0.25} \right)\Omega $$
In case of a meter bridge
$$\eqalign{ & \frac{R}{l} = \frac{X}{{100 - l}}\,{\text{Here}}\,X = 90\Omega ,l = 40.0\;cm \cr & \therefore R = \frac{{Xl}}{{100 - l}} \cr} $$
For finding the value of $$R$$
$$R = \frac{{90 \times 40}}{{60}} = 60\Omega $$
For finding the value of $$\Delta R$$
$$\eqalign{ & \frac{{\Delta R}}{R} = \frac{{\Delta l}}{l} + \frac{{\Delta \left( {100 - l} \right)}}{{100 - l}} \cr & \therefore \frac{{\Delta R}}{{60}} = \frac{{0.1}}{{40}} + \frac{{0.1}}{{60}} \cr & \therefore \Delta R = 0.25\Omega \cr} $$
Therefore, $$R = \left( {60 \pm 0.25} \right)\Omega $$