Question
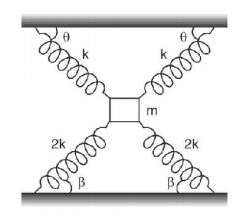
Disregarding gravity, find the period of oscillation of the particle connected with four springs as shown in the figure.
Disregarding gravity, find the period of oscillation of the particle connected with four springs as shown in the figure.
(Given : $$\theta = {45^ \circ },\beta = {30^ \circ }$$ )
A.
$$\pi \sqrt {\frac{{2m}}{k}} $$
B.
$$\sqrt {\frac{{2m\pi }}{k}} $$
C.
$$\sqrt {\frac{{m\pi }}{{2k}}} $$
D.
$$\pi \sqrt {\frac{m}{{2k}}} $$
Answer :
$$\pi \sqrt {\frac{{2m}}{k}} $$
Solution :
$$\eqalign{ & 2k\,{\sin ^2}\theta = {k_1}\,\,{\text{or}}\,\,{k_1} = 2k\,{\sin ^2}\theta \cr & {\text{and}}\,\,{k_2} = 2\left( {2k} \right){\sin ^2}\beta \cr} $$

$$\eqalign{ & {\text{Then}}\,\,{k_{{\text{eq}}}} = {k_1} + {k_2} = 2k\left[ {{{\sin }^2}\theta + 2{{\sin }^2}\beta } \right] \cr & = 2k\left[ {{{\sin }^2}{{45}^ \circ } + 2{{\sin }^2}{{30}^ \circ }} \right] \cr & = 2k\left( {\frac{1}{2} + \frac{1}{2}} \right) = 2k \cr & {\text{Then}}\,\,T = 2\pi \sqrt {\frac{m}{{{k_{{\text{eq}}}}}}} = 2\pi \sqrt {\frac{m}{{2k}}} = \pi \sqrt {\frac{{2m}}{k}} \cr} $$
$$\eqalign{ & 2k\,{\sin ^2}\theta = {k_1}\,\,{\text{or}}\,\,{k_1} = 2k\,{\sin ^2}\theta \cr & {\text{and}}\,\,{k_2} = 2\left( {2k} \right){\sin ^2}\beta \cr} $$

$$\eqalign{ & {\text{Then}}\,\,{k_{{\text{eq}}}} = {k_1} + {k_2} = 2k\left[ {{{\sin }^2}\theta + 2{{\sin }^2}\beta } \right] \cr & = 2k\left[ {{{\sin }^2}{{45}^ \circ } + 2{{\sin }^2}{{30}^ \circ }} \right] \cr & = 2k\left( {\frac{1}{2} + \frac{1}{2}} \right) = 2k \cr & {\text{Then}}\,\,T = 2\pi \sqrt {\frac{m}{{{k_{{\text{eq}}}}}}} = 2\pi \sqrt {\frac{m}{{2k}}} = \pi \sqrt {\frac{{2m}}{k}} \cr} $$