Question

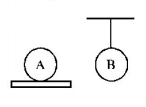
Consider two identical iron spheres , one which lie on a thermally insulating plate, while the other hangs from an insulatory thread. Equal amount of heat is supplied to the two spheres
Conduction mcq question image

A. temperature of $$A$$ will be greater than $$B$$
B. temperature of $$B$$ will be greater than $$A$$  
C. their temperature will be equal
D. can’t be predicted
Answer :   temperature of $$B$$ will be greater than $$A$$
Solution :
Temperature of $$B$$ will be higher because, due to expansion centre of mass $$B$$ will comedown same heat is supplied but in $$B,$$ Potential energy is decreased therefore internal energy gain will be more.

Releted MCQ Question on
Heat and Thermodynamics >> Conduction

Releted Question 1

A wall has two layers $$A$$ and $$B,$$ each made of different material. Both the layers have the same thickness. The thermal conductivity of the meterial of $$A$$ is twice that of $$B.$$ Under thermal equilibrium, the temperature difference across the wall is $${36^ \circ }C.$$  The temperature difference across the layer $$A$$ is

A. $${6^ \circ }C$$
B. $${12^ \circ }C$$
C. $${18^ \circ }C$$
D. $${24^ \circ }C$$
View Answer
Releted Question 2

Three rods of identical cross - sectional area and made from the same metal from the sides of an isosceles triangle $$ABC,$$  right - angled at $$B.$$ The points $$A$$ and $$B$$ are maintained at temperatures $$T$$ and $$\left( {\sqrt 2 } \right)$$  $$T$$ respectively. In the steady state, the temperature of the point $$C$$ is $${T_c}.$$  Assuming that only heat conduction takes place, $$\frac{{{T_c}}}{T}$$ is

A. $$\frac{1}{{2\left( {\sqrt 2 - 1} \right)}}$$
B. $$\frac{3}{{\sqrt 2 + 1}}$$
C. $$\frac{1}{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}$$
D. $$\frac{1}{{\sqrt 2 + 1}}$$
View Answer
Releted Question 3

Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$  and $${90^ \circ }C$$  respectively. The temperature of the junction of the three rods will be
Conduction mcq question image

A. $${45^ \circ }C$$
B. $${60^ \circ }C$$
C. $${30^ \circ }C$$
D. $${20^ \circ }C$$
View Answer
Releted Question 4

Two identical rods are connected between two containers one of them is at $${100^ \circ }C$$  and another is at $${0^ \circ }C.$$  If rods are connected in parallel then the rate of melting of ice is $${q_1}\,gm/sec.$$   If they are connected in series then the rate is $${{q_2}}.$$ The ratio $$\frac{{{q_2}}}{{{q_1}}}$$ is

A. 2
B. 4
C. $$\frac{1}{2}$$
D. $$\frac{1}{4}$$
View Answer

Practice More Releted MCQ Question on
Conduction

Practice More MCQ Question on Physics Section

Basic PhysicsUnit and MeasurementKinematicsLaws of MotionFrictionUniform Circular MotionImpulseMomentumWork Energy and PowerRotational MotionGravitationMechanical Properties of Solids and Fluids
Heat and ThermodynamicsThermodynamicsThermal ExpansionConductionRadiationCalorimetryKinetic Theory of Gases
Electrostatics and MagnetismElectric ChargesElectric FieldElectric PotentialCapacitors and DielectricsMagnetic Effect of CurrentMagnetic MaterialsElectromagnetic WavesElectric CurrentElectromagnetic InductionAlternating CurrentSemiconductors and Electronic Devices
Optics and WaveRay OpticsWave Optics
Modern PhysicsDual Nature of Matter and RadiationAtoms And NucleiAtoms or Nuclear Fission and FusionRadioactivityModern Physics MiscellaneousSemiconductors and Electronic Devices
Oscillation and Mechanical WavesSimple Harmonic Motion (SHM)Waves