Question
Consider a spherical gaseous cloud of mass density $$\rho \left( r \right)$$ in a free space where $$r$$ is the radical distance from its center. The gaseous cloud is made of particles of equal mass $$m$$ moving in circular orbits about the common centre with the same kinetic energy $$K.$$ The force acting on the particles is their mutual gravitational force. If $$\rho \left( r \right)$$ is constant in time. The particle number density $$n\left( r \right) = \rho \left( r \right)/m$$ is-
Consider a spherical gaseous cloud of mass density $$\rho \left( r \right)$$ in a free space where $$r$$ is the radical distance from its center. The gaseous cloud is made of particles of equal mass $$m$$ moving in circular orbits about the common centre with the same kinetic energy $$K.$$ The force acting on the particles is their mutual gravitational force. If $$\rho \left( r \right)$$ is constant in time. The particle number density $$n\left( r \right) = \rho \left( r \right)/m$$ is-
[$$G$$ is universal gravitational constant]
A.
$$\frac{{3K}}{{\pi {r^2}{m^2}G}}$$
B.
$$\frac{K}{{2\pi {r^2}{m^2}G}}$$
C.
$$\frac{K}{{\pi {r^2}{m^2}G}}$$
D.
$$\frac{{3K}}{{6\pi {r^2}{m^2}G}}$$
Answer :
$$\frac{K}{{2\pi {r^2}{m^2}G}}$$
Solution :
The required centripetal force of particle of mass $$'m\,'$$ to revolve in a circular path is provided by gravitational pull of the mass $$'M\,'$$ present in the sphere of radius $$'r\,'$$.
Therefore
$$\eqalign{ & \frac{{m{v^2}}}{r} = \frac{{GMm}}{{{r^2}}}\,\,\, \Rightarrow \frac{1}{2}m{v^2} = \frac{{GMm}}{{2r}}\,\,\, \Rightarrow K = \frac{{GMm}}{{2r}} \cr & \therefore M = \frac{{2Kr}}{{Gm}} \cr} $$
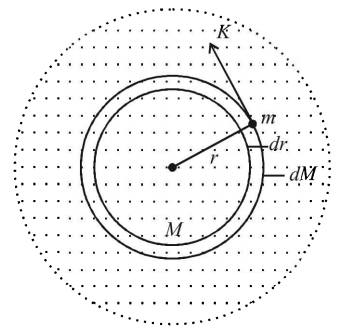
Differentiating the above equation w.r.t $$'r\,'$$ we get
$$\eqalign{ & \frac{{dM}}{{dr}} = \frac{{2K}}{{Gm}}{\text{ or }}dM = \frac{{2K}}{{Gm}}dr \cr & \therefore 4\pi {r^2}dr\rho = \frac{{2K}}{{Gm}}dr \cr & \therefore \rho = \frac{K}{{2\pi {r^2}mG}} \cr & \therefore \frac{\rho }{m} = \frac{K}{{2\pi {r^2}{m^2}G}} \cr} $$
The required centripetal force of particle of mass $$'m\,'$$ to revolve in a circular path is provided by gravitational pull of the mass $$'M\,'$$ present in the sphere of radius $$'r\,'$$.
Therefore
$$\eqalign{ & \frac{{m{v^2}}}{r} = \frac{{GMm}}{{{r^2}}}\,\,\, \Rightarrow \frac{1}{2}m{v^2} = \frac{{GMm}}{{2r}}\,\,\, \Rightarrow K = \frac{{GMm}}{{2r}} \cr & \therefore M = \frac{{2Kr}}{{Gm}} \cr} $$

Differentiating the above equation w.r.t $$'r\,'$$ we get
$$\eqalign{ & \frac{{dM}}{{dr}} = \frac{{2K}}{{Gm}}{\text{ or }}dM = \frac{{2K}}{{Gm}}dr \cr & \therefore 4\pi {r^2}dr\rho = \frac{{2K}}{{Gm}}dr \cr & \therefore \rho = \frac{K}{{2\pi {r^2}mG}} \cr & \therefore \frac{\rho }{m} = \frac{K}{{2\pi {r^2}{m^2}G}} \cr} $$