Consider a collection of a large number of dust particles each with speed $$v.$$ The direction of velocity is randomly distributed in the collection. What is the magnitude of the relative velocity between a pairs in the collection ?

Solution :

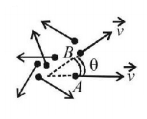
Figure shows the particles each moving with same speed $$v$$ but the different directions. Consider any two particles having angle $$\theta $$ between directions of their velocities.
Then, $$\overrightarrow {{v_{rel}}} = \overrightarrow {{v_B}} - \overrightarrow {{v_A}} $$
$$\eqalign{ & {\text{i}}{\text{.e}}{\text{.,}}\,\,{v_{rel}} = \sqrt {{v^2} + {v^2} - 2vv\cos \theta } \cr & \Rightarrow {v_{rel}} = \sqrt {2{v^2}\left( {1 - \cos \theta } \right)} = 2v\sin \left( {\frac{\theta }{2}} \right) \cr} $$
So averaging $${v_{rel}}$$ over all pairs
$$\eqalign{ & {{\bar v}_{rel}} = \frac{{\int_0^{2\pi } {{v_{rel}}} d\theta }}{{\int_0^{2\pi } d \theta }} = \frac{{\int_0^{2\pi } 2 v\sin \left( {\frac{\theta }{2}} \right)}}{{\int_0^{2\pi } d \theta }} \cr & = \frac{{2v \times 2\left[ { - \cos \left( {\frac{\theta }{2}} \right.} \right]_0^{2\pi }}}{{2\pi }} \cr & \Rightarrow {{\bar v}_{rel}} = \left( {\frac{{4v}}{\pi }} \right) > v\left[ {{\text{as}}\,\frac{4}{\pi } > 1} \right] \cr} $$