Question
An open pipe is in resonance in 2nd harmonic with frequency $${f_1}.$$ Now one end of the tube is closed and frequency is increased to $${f_2}$$ such that the resonance again occurs in $$n$$th harmonic. Choose the correct option
A.
$$n = 3,{f_2} = \frac{3}{4}{f_1}$$
B.
$$n = 3,{f_2} = \frac{5}{4}{f_1}$$
C.
$$n = 5,{f_2} = \frac{3}{4}{f_1}$$
D.
$$n = 5,{f_2} = \frac{5}{4}{f_1}$$
Answer :
$$n = 5,{f_2} = \frac{5}{4}{f_1}$$
Solution :
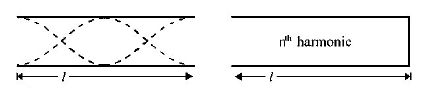
$$\eqalign{ & \lambda = \ell \cr & \therefore {f_1} = \frac{v}{\lambda } = \frac{v}{\ell }\,......\left( {\text{i}} \right) \cr & \lambda = \frac{{4\ell }}{n} \cr & \therefore {f_2} = \frac{v}{\lambda } = \frac{{nv}}{{4\ell }}\,......\left( {{\text{ii}}} \right) \cr} $$
Here $$n$$ is a odd number. From (i) and (ii)
$${f_2} = \frac{n}{4}{f_1}$$
For first resonance, $$n = 5,{f_2} = \frac{5}{4}{f_1}$$

$$\eqalign{ & \lambda = \ell \cr & \therefore {f_1} = \frac{v}{\lambda } = \frac{v}{\ell }\,......\left( {\text{i}} \right) \cr & \lambda = \frac{{4\ell }}{n} \cr & \therefore {f_2} = \frac{v}{\lambda } = \frac{{nv}}{{4\ell }}\,......\left( {{\text{ii}}} \right) \cr} $$
Here $$n$$ is a odd number. From (i) and (ii)
$${f_2} = \frac{n}{4}{f_1}$$
For first resonance, $$n = 5,{f_2} = \frac{5}{4}{f_1}$$