Releted MCQ Question on
Electrostatics and Magnetism >> Alternating Current
Releted Question 1
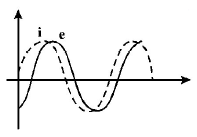
When an $$AC$$ source of emf $$e = {E_0}\sin \left( {100t} \right)$$ is connected across a circuit, the phase difference between the emf $$e$$ and the current $$i$$ in the circuit is observed to be $$\frac{\pi }{4},$$ as shown in the diagram. If the circuit consists possibly only of $$R - C$$ or $$R - L$$ or $$L - C$$ in series, find the relationship between the two elements
When an $$AC$$ source of emf $$e = {E_0}\sin \left( {100t} \right)$$ is connected across a circuit, the phase difference between the emf $$e$$ and the current $$i$$ in the circuit is observed to be $$\frac{\pi }{4},$$ as shown in the diagram. If the circuit consists possibly only of $$R - C$$ or $$R - L$$ or $$L - C$$ in series, find the relationship between the two elements
A.
$$R = 1k\Omega ,C = 10\mu F$$
B.
$$R = 1k\Omega ,C = 1\mu F$$
C.
$$R = 1k\Omega ,L = 10H$$
D.
$$R = 1k\Omega ,L = 1H$$
Releted Question 2
An $$AC$$ voltage source of variable angular frequency $$\omega $$ and fixed amplitude $${V_0}$$ is connected in series with a capacitance $$C$$ and an electric bulb of resistance $$R$$ (inductance zero). When $$\omega $$ is increase
A.
the bulb glows dimmer
B.
the bulb glows brighter
C.
total impedance of the circuit is unchanged
D.
total impedance of the circuit increases
Releted Question 3
In a transformer, number of turns in the primary coil are 140 and that in the secondary coil are 280. If current in primary coil is $$4A,$$ then that in the secondary coil is
A.
$$4 A$$
B.
$$2 A$$
C.
$$6 A$$
D.
$$10 A$$
Releted Question 4
The core of any transformer is laminated so as to
A.
reduce the energy loss due to eddy currents
B.
make it light weight
C.
make it robust and strong
D.
increase the secondary voltage