Question
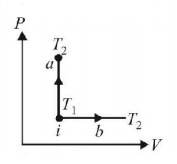
An ideal gas has temperature $${T_1}$$ at the initial state i shown in the $$P-V$$ diagram. The gas has a higher temperature $${T_2}$$ at the final states $$a$$ and $$b,$$ which it can reach the paths shown. The change in entropy:
An ideal gas has temperature $${T_1}$$ at the initial state i shown in the $$P-V$$ diagram. The gas has a higher temperature $${T_2}$$ at the final states $$a$$ and $$b,$$ which it can reach the paths shown. The change in entropy:
A.
greatest in $$a$$
B.
greatest in $$b$$
C.
same in $$a$$ and $$b$$
D.
nothing can be said
Answer :
greatest in $$b$$
Solution :
$$\eqalign{ & {Q_a} = \Delta U + 0 = \Delta U\,\,{\text{and}}\,\,{Q_b} = \Delta U + P\Delta V \cr & {\text{As}}\,\,{Q_b} > {Q_a} \cr} $$
∴ Change in entropy is greater in case (b).
$$\eqalign{ & {Q_a} = \Delta U + 0 = \Delta U\,\,{\text{and}}\,\,{Q_b} = \Delta U + P\Delta V \cr & {\text{As}}\,\,{Q_b} > {Q_a} \cr} $$
∴ Change in entropy is greater in case (b).