Question
A wire of length $$L$$ and 3 identical cells of negligible internal resistances are connected in series. Due to the current, the temperature of the wire is raised by $$\Delta T$$ in a time $$t.$$ A number $$N$$ of similar cells is now connected in series with a wire of the same material and cross-section but of length $$2L.$$ The temperature of the wire is raised by the same amount $$\Delta T$$ in the same time $$t.$$ the value of $$N$$ is
A.
4
B.
6
C.
8
D.
9
Answer :
6
Solution :
Let $$R$$ be the resistance of wire.
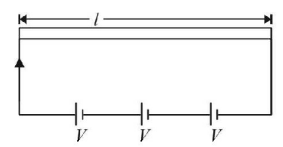
Energy released in $$t$$ second $$ = \frac{{{{\left( {3V} \right)}^2}}}{R} \times t$$
$$\eqalign{ & \therefore Q = \frac{{9{V^2}}}{R} \times t \cr & \therefore mc\Delta T = \frac{{9{V^2}}}{R} \times t\,\,\left( {\because But\,Q = mc\Delta T} \right)\,......\left( {\text{i}} \right) \cr} $$
Let $$R'$$ be the resistance of the second wire
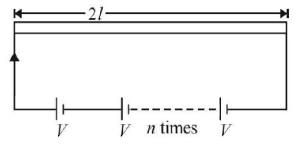
$$ \Rightarrow R' = 2R\,\,\,\,\,\,\left( {\because {\text{length}}\,{\text{is}}\,{\text{twice}}} \right)$$
∴ Energy released in $$t$$-seconds $$ = \frac{{{{\left( {NV} \right)}^2}}}{{2R}} \times t$$
$$\eqalign{ & {\text{Also}}\,Q' = m'c\Delta T = \left( {2m} \right)C\Delta T \cr & 2mc\Delta T = \frac{{{N^2}{V^2}}}{{2R}} \times t\,......\left( {{\text{ii}}} \right) \cr} $$
Dividing (i) by (ii)
$$\eqalign{ & \frac{{mc\Delta T}}{{2mc\Delta T}} = \frac{{\frac{{9{V^2} \times t}}{R}}}{{\frac{{{N^2}{V^2} \times t}}{{2R}}}}\,\,\,{\text{or,}}\,\,\,\,\frac{1}{2} = \frac{{9 \times 2}}{{{N^2}}} \cr & {\text{or,}}\,{N^2} = 18 \times 2\,\,\,\,\,\therefore N = 6 \cr} $$
Let $$R$$ be the resistance of wire.

Energy released in $$t$$ second $$ = \frac{{{{\left( {3V} \right)}^2}}}{R} \times t$$
$$\eqalign{ & \therefore Q = \frac{{9{V^2}}}{R} \times t \cr & \therefore mc\Delta T = \frac{{9{V^2}}}{R} \times t\,\,\left( {\because But\,Q = mc\Delta T} \right)\,......\left( {\text{i}} \right) \cr} $$
Let $$R'$$ be the resistance of the second wire

$$ \Rightarrow R' = 2R\,\,\,\,\,\,\left( {\because {\text{length}}\,{\text{is}}\,{\text{twice}}} \right)$$
∴ Energy released in $$t$$-seconds $$ = \frac{{{{\left( {NV} \right)}^2}}}{{2R}} \times t$$
$$\eqalign{ & {\text{Also}}\,Q' = m'c\Delta T = \left( {2m} \right)C\Delta T \cr & 2mc\Delta T = \frac{{{N^2}{V^2}}}{{2R}} \times t\,......\left( {{\text{ii}}} \right) \cr} $$
Dividing (i) by (ii)
$$\eqalign{ & \frac{{mc\Delta T}}{{2mc\Delta T}} = \frac{{\frac{{9{V^2} \times t}}{R}}}{{\frac{{{N^2}{V^2} \times t}}{{2R}}}}\,\,\,{\text{or,}}\,\,\,\,\frac{1}{2} = \frac{{9 \times 2}}{{{N^2}}} \cr & {\text{or,}}\,{N^2} = 18 \times 2\,\,\,\,\,\therefore N = 6 \cr} $$