Releted MCQ Question on
Basic Physics >> Mechanical Properties of Solids and Fluids
Releted Question 1
The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied?
A.
$$length=50\,cm, \,\,diameter=0.5 \,mm$$
B.
$$length = 100 \,cm, \,\,diameter= 1 \,mm$$
C.
$$length= 200 \,cm, \,\,diameter= 2 \,mm$$
D.
$$length=300 \,cm, \,\,diameter =3 \,mm$$
Releted Question 2
A U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by $$2 \,cm.$$ If the specific gravity of liquid I is $$1.1,$$ the specific gravity of liquid II must be-
A U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by $$2 \,cm.$$ If the specific gravity of liquid I is $$1.1,$$ the specific gravity of liquid II must be-
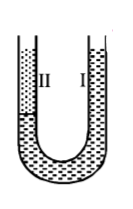
A.
$$1.12$$
B.
$$1.1$$
C.
$$1.05$$
D.
$$1.0$$
Releted Question 3
A homogeneous solid cylinder of length $$L\left( {L < \frac{H}{2}} \right),$$ cross-sectional area $$\frac{A}{5}$$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $$\frac{L}{4}$$ in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure $${P_0}.$$ Then density $$D$$ of solid is given by-
A homogeneous solid cylinder of length $$L\left( {L < \frac{H}{2}} \right),$$ cross-sectional area $$\frac{A}{5}$$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $$\frac{L}{4}$$ in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure $${P_0}.$$ Then density $$D$$ of solid is given by-
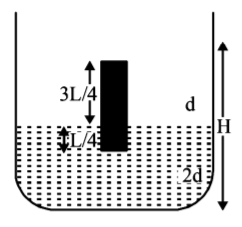
A.
$$\frac{5}{4}d$$
B.
$$\frac{4}{5}d$$
C.
$$4d$$
D.
$$\frac{d}{5}$$
Releted Question 4
A large open tank has two holes in the wall. One is a square hole of side $$L$$ at a depth $$y$$ from the top and the other is a circular hole of radius $$R$$ at a depth $$4y$$ from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, $$R$$ is equal to-
A.
$$\frac{L}{{\sqrt {2\pi } }}$$
B.
$$2\pi L$$
C.
$$L$$
D.
$$\frac{L}{{2\pi }}$$