Question
A wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is $${v_{CM}},$$ then true statement is
A wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is $${v_{CM}},$$ then true statement is
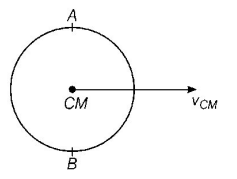
A.
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero
B.
The velocity of point $$A$$ is zero and velocity of point $$B$$ is $$2{v_{CM}}$$
C.
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is $$ - {v_{CM}}$$
D.
The velocities of both $$A$$ and $$B$$ are $${v_{CM}}$$
Answer :
The velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero
Solution :
Similarly, velocity of point $$A$$ is given by
$${v_{AB}} = {\text{velocity of centre of mass}}\left( {{v_{CM}}} \right) + {\text{Linear velocity of point }}A\left( {R\omega } \right){\text{ }}$$
$$\eqalign{ & = {v_{CM}} + {v_{CM}}\,\,\left( {\because {v_{CM}} = R\omega } \right) \cr & = 2{v_{CM}} \cr} $$
Velocity of point $$B$$ is,
$$\eqalign{ & {v_B} = {v_{CM}} - R\omega \cr & = {v_{CM}} - {v_{CM}} \cr & = 0 \cr} $$
Thus, the velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero.
Similarly, velocity of point $$A$$ is given by
$${v_{AB}} = {\text{velocity of centre of mass}}\left( {{v_{CM}}} \right) + {\text{Linear velocity of point }}A\left( {R\omega } \right){\text{ }}$$
$$\eqalign{ & = {v_{CM}} + {v_{CM}}\,\,\left( {\because {v_{CM}} = R\omega } \right) \cr & = 2{v_{CM}} \cr} $$
Velocity of point $$B$$ is,
$$\eqalign{ & {v_B} = {v_{CM}} - R\omega \cr & = {v_{CM}} - {v_{CM}} \cr & = 0 \cr} $$
Thus, the velocity of point $$A$$ is $$2{v_{CM}}$$ and velocity of point $$B$$ is zero.