Question
A uniform wooden stick of mass $$1.6 \,kg$$ and length $$l$$ rests in an inclined manner on a smooth, vertical wall of height $$h\left( { < l} \right)$$ such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $${30^ \circ }$$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $$\frac{h}{l}$$ and the frictional force $$f$$ at the bottom of the stick are-
A uniform wooden stick of mass $$1.6 \,kg$$ and length $$l$$ rests in an inclined manner on a smooth, vertical wall of height $$h\left( { < l} \right)$$ such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $${30^ \circ }$$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $$\frac{h}{l}$$ and the frictional force $$f$$ at the bottom of the stick are-
$$\left( {g = 10\,m{s^{ - 2}}} \right)$$
A.
$$\frac{h}{l} = \frac{{\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
B.
$$\frac{h}{l} = \frac{3}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
C.
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{8\sqrt 3 }}{3}N$$
D.
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
Answer :
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
Solution :
Considering the normal reaction of the floor and wall to be $$N$$ and with reference to the figure.
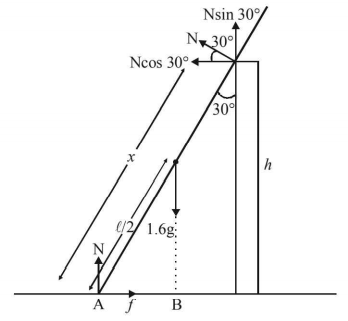
By vertical equilibrium
$$N + N\sin {30^ \circ } = 1.6\,g\,\,\, \Rightarrow N = \frac{{3.2g}}{3}\,\,.....(i)$$
By horizontal equilibrium
$$f = N\cos {30^ \circ } = \frac{{\sqrt 3 }}{2}N = \frac{{16\sqrt 3 }}{3}\,{\text{From }}(i)$$
Taking torque about $$A$$ we get
$$\eqalign{ & 1.6g \times AB = N \times x \cr & 1.6g \times \frac{\ell }{2}\cos {60^ \circ } = \frac{{3.2g}}{3} \times x \cr & \therefore \frac{{3\ell }}{8} = x\,\,.....(ii) \cr & {\text{But }}\cos {30^ \circ } = \frac{h}{x} \cr & \therefore x = \frac{h}{{\cos {{30}^ \circ }}}\,\,\,.....(iii) \cr & {\text{From }}(ii)\,\,{\text{and }}(iii) \cr & \frac{h}{{\cos {{30}^ \circ }}} = \frac{{3\ell }}{8} \cr & \therefore \frac{h}{\ell } = \frac{{3\sqrt 3 }}{{16}} \cr} $$
Considering the normal reaction of the floor and wall to be $$N$$ and with reference to the figure.

By vertical equilibrium
$$N + N\sin {30^ \circ } = 1.6\,g\,\,\, \Rightarrow N = \frac{{3.2g}}{3}\,\,.....(i)$$
By horizontal equilibrium
$$f = N\cos {30^ \circ } = \frac{{\sqrt 3 }}{2}N = \frac{{16\sqrt 3 }}{3}\,{\text{From }}(i)$$
Taking torque about $$A$$ we get
$$\eqalign{ & 1.6g \times AB = N \times x \cr & 1.6g \times \frac{\ell }{2}\cos {60^ \circ } = \frac{{3.2g}}{3} \times x \cr & \therefore \frac{{3\ell }}{8} = x\,\,.....(ii) \cr & {\text{But }}\cos {30^ \circ } = \frac{h}{x} \cr & \therefore x = \frac{h}{{\cos {{30}^ \circ }}}\,\,\,.....(iii) \cr & {\text{From }}(ii)\,\,{\text{and }}(iii) \cr & \frac{h}{{\cos {{30}^ \circ }}} = \frac{{3\ell }}{8} \cr & \therefore \frac{h}{\ell } = \frac{{3\sqrt 3 }}{{16}} \cr} $$