Question
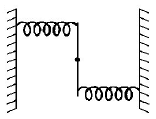
A uniform rod of length $$L$$ and mass $$M$$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $$k.$$ The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $$\theta $$ in one direction and released. The frequency of oscillation is
A uniform rod of length $$L$$ and mass $$M$$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $$k.$$ The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $$\theta $$ in one direction and released. The frequency of oscillation is
A.
$$\frac{1}{{2\pi }}\sqrt {\frac{{2k}}{M}} $$
B.
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{M}} $$
C.
$$\frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} $$
D.
$$\frac{1}{{2\pi }}\sqrt {\frac{{24k}}{M}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} $$
Solution :
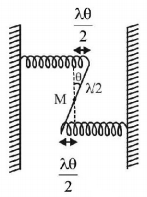
Figure shows the rod at an angle $$\theta $$ with respect to its equilibrium position. Both the springs are stretched by length $$\frac{{\ell \theta }}{2}.$$
The restoring torque due to the springs $$\tau = - 2{\text{(Restoring force)}} \times {\text{perpendicular distance}}$$
$$\tau = - 2k\left( {\frac{{\ell \theta }}{2}} \right) \times \frac{\ell }{2} = - k\frac{{{\ell ^2}}}{2}\theta \,......\left( {\text{i}} \right)$$
If $$I$$ is the moment of inertia of the rod about $$M$$ then
$$\tau = I\alpha = I\frac{{{d^2}\theta }}{{d{t^2}}}\,......\left( {{\text{ii}}} \right)$$
From (i) & (ii) we get
$$\eqalign{ & I\frac{{{d^2}\theta }}{{d{t^2}}} = - k\frac{{{\ell ^2}\theta }}{2} \Rightarrow \frac{{{d^2}\theta }}{{d{t^2}}} = - \frac{k}{I}\frac{{{\ell ^2}}}{2}\theta = \frac{{ - k}}{{\frac{{M{\ell ^2}}}{{12}}}}\frac{{{\ell ^2}}}{2}\theta \cr & \Rightarrow \frac{{{d^2}\theta }}{{d{t^2}}} = - \frac{{6k}}{M}\theta \cr} $$
Comparing it with the standard equation of rotational SHM we get
$$\eqalign{ & \frac{{{d^2}\theta }}{{d{t^2}}} = - {\omega ^2}\theta \Rightarrow {\omega ^2} = \frac{{6k}}{M} \Rightarrow \omega = \sqrt {\frac{{6k}}{M}} \cr & \Rightarrow 2\pi v = \sqrt {\frac{{6k}}{M}} \Rightarrow v = \frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} \cr} $$

Figure shows the rod at an angle $$\theta $$ with respect to its equilibrium position. Both the springs are stretched by length $$\frac{{\ell \theta }}{2}.$$
The restoring torque due to the springs $$\tau = - 2{\text{(Restoring force)}} \times {\text{perpendicular distance}}$$
$$\tau = - 2k\left( {\frac{{\ell \theta }}{2}} \right) \times \frac{\ell }{2} = - k\frac{{{\ell ^2}}}{2}\theta \,......\left( {\text{i}} \right)$$
If $$I$$ is the moment of inertia of the rod about $$M$$ then
$$\tau = I\alpha = I\frac{{{d^2}\theta }}{{d{t^2}}}\,......\left( {{\text{ii}}} \right)$$
From (i) & (ii) we get
$$\eqalign{ & I\frac{{{d^2}\theta }}{{d{t^2}}} = - k\frac{{{\ell ^2}\theta }}{2} \Rightarrow \frac{{{d^2}\theta }}{{d{t^2}}} = - \frac{k}{I}\frac{{{\ell ^2}}}{2}\theta = \frac{{ - k}}{{\frac{{M{\ell ^2}}}{{12}}}}\frac{{{\ell ^2}}}{2}\theta \cr & \Rightarrow \frac{{{d^2}\theta }}{{d{t^2}}} = - \frac{{6k}}{M}\theta \cr} $$
Comparing it with the standard equation of rotational SHM we get
$$\eqalign{ & \frac{{{d^2}\theta }}{{d{t^2}}} = - {\omega ^2}\theta \Rightarrow {\omega ^2} = \frac{{6k}}{M} \Rightarrow \omega = \sqrt {\frac{{6k}}{M}} \cr & \Rightarrow 2\pi v = \sqrt {\frac{{6k}}{M}} \Rightarrow v = \frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} \cr} $$