Question
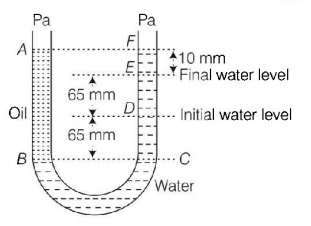
A $$U$$ tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of $$10\,mm$$ above the water level on the other side. Meanwhile the water rises by $$65\,mm$$ from its original level (see diagram). The density of the oil is
A $$U$$ tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of $$10\,mm$$ above the water level on the other side. Meanwhile the water rises by $$65\,mm$$ from its original level (see diagram). The density of the oil is
A.
$$650\,kg\,{m^{ - 3}}$$
B.
$$425\,kg\,{m^{ - 3}}$$
C.
$$800\,kg\,{m^{ - 3}}$$
D.
$$928\,kg\,{m^{ - 3}}$$
Answer :
$$928\,kg\,{m^{ - 3}}$$
Solution :
Pressure of two points lie in the same horizontal level should be same and $$p = hdg$$
Both ends of the $$U$$ tube are open, so the pressure on both the free surfaces must be equal.
i.e., $${p_1} = {p_2}$$
$$\eqalign{ & {h_{{\text{oil}}}} \cdot {S_{{\text{oil}}}}\,g = {h_{{\text{water}}}} \cdot {S_{{\text{water}}}} \cdot g \cr & {S_{{\text{oil}}}} = {\text{specific density of}}\,{\text{oil}} \cr & {S_{{\text{oil}}}} = \frac{{{h_{{\text{water}}}} \cdot {S_{{\text{water}}}} \cdot g}}{{{h_{{\text{oil}}}} \cdot g}} \cr} $$
From figure $${S_{{\text{oil}}}} = \frac{{\left( {65 + 65} \right) \times 1000}}{{\left( {65 + 65 + 10} \right)}}$$
$$ = 928\,kg{m^{ - 3}}$$
Pressure of two points lie in the same horizontal level should be same and $$p = hdg$$
Both ends of the $$U$$ tube are open, so the pressure on both the free surfaces must be equal.
i.e., $${p_1} = {p_2}$$
$$\eqalign{ & {h_{{\text{oil}}}} \cdot {S_{{\text{oil}}}}\,g = {h_{{\text{water}}}} \cdot {S_{{\text{water}}}} \cdot g \cr & {S_{{\text{oil}}}} = {\text{specific density of}}\,{\text{oil}} \cr & {S_{{\text{oil}}}} = \frac{{{h_{{\text{water}}}} \cdot {S_{{\text{water}}}} \cdot g}}{{{h_{{\text{oil}}}} \cdot g}} \cr} $$
From figure $${S_{{\text{oil}}}} = \frac{{\left( {65 + 65} \right) \times 1000}}{{\left( {65 + 65 + 10} \right)}}$$
$$ = 928\,kg{m^{ - 3}}$$