A transparent solid cylindrical rod has a refractive index of $${\frac{2}{{\sqrt 3 }}}.$$  It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure.

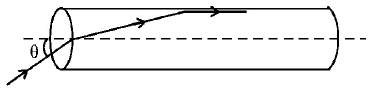
The incident angle $$\theta $$ for which the light ray grazes along the wall of the rod is:

Solution :

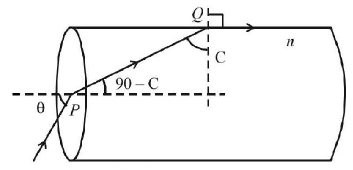
Applying Snell’s law at $$Q$$
$$\eqalign{ & n = \frac{{\sin {{90}^ \circ }}}{{\sin C}} = \frac{1}{{\sin C}} \cr & \therefore \,\,\sin C = \frac{1}{n} = \frac{{\sqrt 3 }}{2} \cr & \therefore \,\,C = {60^ \circ } \cr} $$
Applying Snell’s Law at $$P$$
$$\eqalign{ & n = \frac{{\sin \theta }}{{\sin \left( {{{90}^ \circ } - C} \right)}} \cr & \Rightarrow \,\,\sin \theta = n \times \sin \left( {{{90}^ \circ } - C} \right);\,{\text{from }}\left( 1 \right) \cr & \Rightarrow \,\,\sin \theta = n\cos \cr & \therefore \,\,\theta = {\sin ^{ - 1}}\left[ {\frac{2}{{\sqrt 3 }} \times \cos {{60}^ \circ }} \right] \cr & {\text{or, }}\theta = {\sin ^{ - 1}}\left( {\frac{1}{{\sqrt 3 }}} \right) \cr} $$