Question
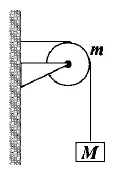
A string of negligible mass going over a damped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by
A string of negligible mass going over a damped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by
A.
$$\sqrt 2 \,{\text{Mg}}$$
B.
$$\sqrt 2 \,{\text{mg}}$$
C.
$$\sqrt {{{\left( {M + m} \right)}^2} + {m^2}} g$$
D.
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
Answer :
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
Solution :
At equilibrium $$T = Mg$$

F.B.D. of pulley
$${F_1} = \left( {m + M} \right)g$$
The resultant force on pulley is
$$F = \sqrt {F_1^2 + {T^2}} = \left[ {\sqrt {{{\left( {m + M} \right)}^2} + {M^2}} } \right]g$$
At equilibrium $$T = Mg$$

F.B.D. of pulley
$${F_1} = \left( {m + M} \right)g$$
The resultant force on pulley is
$$F = \sqrt {F_1^2 + {T^2}} = \left[ {\sqrt {{{\left( {m + M} \right)}^2} + {M^2}} } \right]g$$