Question
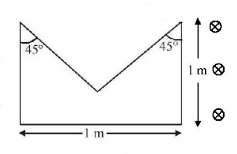
A straight conducting metal wire is bent in the given shape and the loop is closed. Dimensions are as shown in the figure. Now the assembly is heated at a constant rate $$\frac{{dT}}{{dt}} = {1^ \circ }C/s.$$ The assembly is kept in a uniform magnetic field $$B = 1\,T,$$ perpendicular into the paper. Find the current in the loop at the moment, when the heating starts. Resistance of the loop is $$10\,\Omega $$ at any temperature. Coefficient of linear expansion $$\alpha = \frac{{{{10}^{ - 6}}}}{{^ \circ C}}.$$
A straight conducting metal wire is bent in the given shape and the loop is closed. Dimensions are as shown in the figure. Now the assembly is heated at a constant rate $$\frac{{dT}}{{dt}} = {1^ \circ }C/s.$$ The assembly is kept in a uniform magnetic field $$B = 1\,T,$$ perpendicular into the paper. Find the current in the loop at the moment, when the heating starts. Resistance of the loop is $$10\,\Omega $$ at any temperature. Coefficient of linear expansion $$\alpha = \frac{{{{10}^{ - 6}}}}{{^ \circ C}}.$$
A.
$$1.5 \times {10^{ - 6}}A\,{\text{anticlockwise}}$$
B.
$$1.5 \times {10^{ - 6}}A\,{\text{clockwise}}$$
C.
$$0.75 \times {10^{ - 6}}A\,{\text{anticlockwise}}$$
D.
$$0.75 \times {10^{ - 6}}A\,{\text{clockwise}}$$
Answer :
$$1.5 \times {10^{ - 6}}A\,{\text{anticlockwise}}$$
Solution :
Rate of change of area of the loop
$$\eqalign{ & \frac{{dA}}{{dt}} = A,\beta \frac{{dT}}{{dt}} = A.\left( {2\alpha } \right)\frac{{dT}}{{dt}} = \frac{3}{4} \times 2 \times {10^{ - 6}} \times 1 \cr & = 11.5 \times {10^{ - 6}}{m^2}/s \cr & {\text{emf}} = - \frac{{d\phi }}{{dt}} = - \frac{{\beta .dA}}{{dt}} = - 1.5 \times {10^{ - 6}}V \cr} $$
current in the loop $$ = 1.5 \times {10^{ - 6}}A$$
The direction will be anticlockwise as the induced current will try to negate the increase in fluix due to increase in area.
Rate of change of area of the loop
$$\eqalign{ & \frac{{dA}}{{dt}} = A,\beta \frac{{dT}}{{dt}} = A.\left( {2\alpha } \right)\frac{{dT}}{{dt}} = \frac{3}{4} \times 2 \times {10^{ - 6}} \times 1 \cr & = 11.5 \times {10^{ - 6}}{m^2}/s \cr & {\text{emf}} = - \frac{{d\phi }}{{dt}} = - \frac{{\beta .dA}}{{dt}} = - 1.5 \times {10^{ - 6}}V \cr} $$
current in the loop $$ = 1.5 \times {10^{ - 6}}A$$
The direction will be anticlockwise as the induced current will try to negate the increase in fluix due to increase in area.
