Question
A standing wave having $$3$$ node and $$2$$ antinode is formed between two atoms having a distance $$1.21\,\mathop {\text{A}}\limits^ \circ $$ between them. The wavelength of the standing wave is
A.
$$1.21\,\mathop {\text{A}}\limits^ \circ $$
B.
$$1.42\,\mathop {\text{A}}\limits^ \circ $$
C.
$$6.05\,\mathop {\text{A}}\limits^ \circ $$
D.
$$3.63\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$1.21\,\mathop {\text{A}}\limits^ \circ $$
Solution :
The given standing wave is shown in the figure.
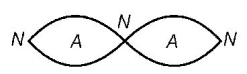
As length of one loop or segment is $$\frac{\lambda }{2},$$ so length of $$2$$ segments is $$2\left( {\frac{\lambda }{2}} \right).$$
So, according to question
$$\therefore 2\frac{\lambda }{2} = 1.21\,\mathop {\text{A}}\limits^ \circ \Rightarrow \lambda = 1.21\,\mathop {\text{A}}\limits^ \circ $$
The given standing wave is shown in the figure.
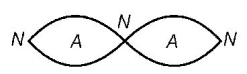
As length of one loop or segment is $$\frac{\lambda }{2},$$ so length of $$2$$ segments is $$2\left( {\frac{\lambda }{2}} \right).$$
So, according to question
$$\therefore 2\frac{\lambda }{2} = 1.21\,\mathop {\text{A}}\limits^ \circ \Rightarrow \lambda = 1.21\,\mathop {\text{A}}\limits^ \circ $$