Question
A solid sphere of mass $$'M\,'$$ and radius $$'a\,'$$ is surrounded by a uniform concentric spherical shell of thickness $$2a$$ and mass $$2M.$$ The gravitational field at distance $$'3a\,'$$ from the centre will be:
A.
$$\frac{{2GM}}{{9{a^2}}}$$
B.
$$\frac{{GM}}{{9{a^2}}}$$
C.
$$\frac{{GM}}{{3{a^2}}}$$
D.
$$\frac{{2GM}}{{3{a^2}}}$$
Answer :
$$\frac{{GM}}{{3{a^2}}}$$
Solution :
$${E_P} = \frac{{GM}}{{{{\left( {3a} \right)}^2}}} + \frac{{G\left( {2M} \right)}}{{{{\left( {3a} \right)}^2}}} = \frac{{GM}}{{3{a^2}}}$$
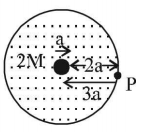
For a part on the surface of a spherical uniform charge distribution the whole mass acts as a point mass kept at the centre.
$${E_P} = \frac{{GM}}{{{{\left( {3a} \right)}^2}}} + \frac{{G\left( {2M} \right)}}{{{{\left( {3a} \right)}^2}}} = \frac{{GM}}{{3{a^2}}}$$

For a part on the surface of a spherical uniform charge distribution the whole mass acts as a point mass kept at the centre.