Question
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface
(see figure).
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface
(see figure).
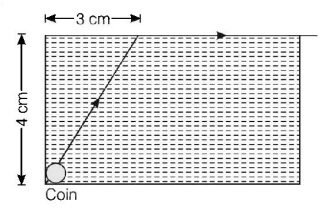
How fast is the light travelling in the liquid?
A.
$$1.8 \times {10^8}m/s$$
B.
$$2.4 \times {10^8}m/s$$
C.
$$3.0 \times {10^8}m/s$$
D.
$$1.2 \times {10^4}m/s$$
Answer :
$$1.8 \times {10^8}m/s$$
Solution :
As shown in figure, a light ray from the coin will not emerge out of liquid, if $$i > C.$$
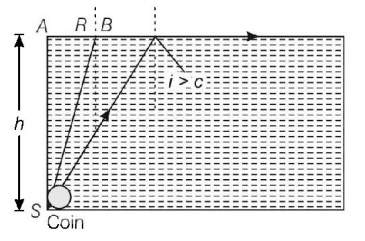
Therefore, minimum radius $$R$$ corresponds to $$i = C.$$
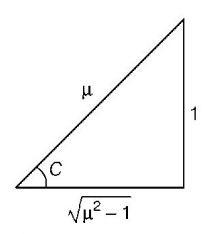
In $$\Delta SAB,$$
$$\eqalign{ & \frac{R}{h} = \tan C \cr & {\text{or}}\,\,R = h\tan C \cr & {\text{or}}\,\,R = \frac{h}{{\sqrt {{\mu ^2} - 1} }} \cr & {\text{Given,}}\,\,R = 3\,cm,h = 4\,cm \cr & {\text{Hence,}}\,\,\frac{3}{4} = \frac{1}{{\sqrt {{\mu ^2} - 1} }} \cr & {\text{or}}\,\,{\mu ^2} = \frac{{25}}{9}\,\,{\text{or }}\mu = \frac{5}{3} \cr & {\text{But}}\,\,\mu = \frac{c}{v}\,\,{\text{or}}\,\,v = \frac{c}{\mu } \cr & = \frac{{3 \times {{10}^8}}}{{\frac{5}{3}}} \cr & = 1.8 \times {10^8}\,m/s \cr} $$
As shown in figure, a light ray from the coin will not emerge out of liquid, if $$i > C.$$

Therefore, minimum radius $$R$$ corresponds to $$i = C.$$

In $$\Delta SAB,$$
$$\eqalign{ & \frac{R}{h} = \tan C \cr & {\text{or}}\,\,R = h\tan C \cr & {\text{or}}\,\,R = \frac{h}{{\sqrt {{\mu ^2} - 1} }} \cr & {\text{Given,}}\,\,R = 3\,cm,h = 4\,cm \cr & {\text{Hence,}}\,\,\frac{3}{4} = \frac{1}{{\sqrt {{\mu ^2} - 1} }} \cr & {\text{or}}\,\,{\mu ^2} = \frac{{25}}{9}\,\,{\text{or }}\mu = \frac{5}{3} \cr & {\text{But}}\,\,\mu = \frac{c}{v}\,\,{\text{or}}\,\,v = \frac{c}{\mu } \cr & = \frac{{3 \times {{10}^8}}}{{\frac{5}{3}}} \cr & = 1.8 \times {10^8}\,m/s \cr} $$