Question
A ship $$A$$ is moving Westwards with a speed of $$10\,km\,{h^{ - 1}}$$ and a ship $$B$$ $$100\,km$$ South of $$A,$$ is moving Northwards with a speed of $$10\,km\,{h^{ - 1}}.$$ The time after which the distance between them becomes shortest is
A.
$$0\,h$$
B.
$$5\,h$$
C.
$$5\sqrt 2 \,h$$
D.
$$10\sqrt 2 \,h$$
Answer :
$$5\,h$$
Solution :
It is clear from the diagram that the shortest distance between the ship $$A$$ and $$B$$ is $$PQ.$$
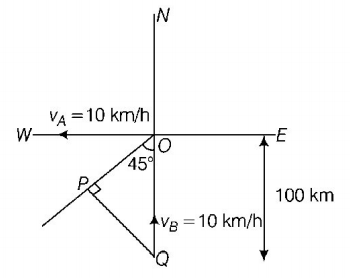
Here, $$\sin {45^ \circ } = \frac{{PQ}}{{OQ}} \Rightarrow PQ = 100 \times \frac{1}{{\sqrt 2 }} = 50\sqrt 2 \,m$$
Also, $${v_{AB}} = \sqrt {v_A^2 + v_B^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 \,km/h$$
So, time taken for them to reach shortest path is
$$t = \frac{{PQ}}{{{v_{AB}}}} = \frac{{50\sqrt 2 }}{{10\sqrt 2 }} = 5\,h$$
It is clear from the diagram that the shortest distance between the ship $$A$$ and $$B$$ is $$PQ.$$

Here, $$\sin {45^ \circ } = \frac{{PQ}}{{OQ}} \Rightarrow PQ = 100 \times \frac{1}{{\sqrt 2 }} = 50\sqrt 2 \,m$$
Also, $${v_{AB}} = \sqrt {v_A^2 + v_B^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 \,km/h$$
So, time taken for them to reach shortest path is
$$t = \frac{{PQ}}{{{v_{AB}}}} = \frac{{50\sqrt 2 }}{{10\sqrt 2 }} = 5\,h$$