Question
A satellite is launched in the equatorial plane in such a way that it can transmit signals upto $${60^ \circ }$$ latitude on the earth. The angular velocity of the satellite is
A.
$$\sqrt {\frac{{GM}}{{8{R^3}}}} $$
B.
$$\sqrt {\frac{{GM}}{{2{R^3}}}} $$
C.
$$\sqrt {\frac{{GM}}{{4{R^3}}}} $$
D.
$$\sqrt {\frac{{3\sqrt 3 GM}}{{8{R^3}}}} $$
Answer :
$$\sqrt {\frac{{GM}}{{8{R^3}}}} $$
Solution :
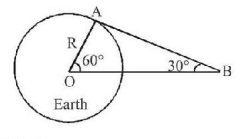
In $$\Delta AOB:\cos {60^ \circ } = \frac{R}{{OB}} \Rightarrow OB = 2R$$
Here gravitational force will provide the required centripetal force.
Hence, $$\frac{{GMm}}{{{{\left( {OB} \right)}^2}}} = m\left( {OB} \right){\omega ^2}$$
$$ \Rightarrow \omega = \sqrt {\frac{{GM}}{{{{\left( {OB} \right)}^3}}}} = \sqrt {\frac{{GM}}{{{{\left( {2R} \right)}^3}}}} \Rightarrow \omega = \sqrt {\frac{{GM}}{{8{R^3}}}} $$

In $$\Delta AOB:\cos {60^ \circ } = \frac{R}{{OB}} \Rightarrow OB = 2R$$
Here gravitational force will provide the required centripetal force.
Hence, $$\frac{{GMm}}{{{{\left( {OB} \right)}^2}}} = m\left( {OB} \right){\omega ^2}$$
$$ \Rightarrow \omega = \sqrt {\frac{{GM}}{{{{\left( {OB} \right)}^3}}}} = \sqrt {\frac{{GM}}{{{{\left( {2R} \right)}^3}}}} \Rightarrow \omega = \sqrt {\frac{{GM}}{{8{R^3}}}} $$