Question
A rope is wound around a hollow cylinder of mass $$3\,kg$$ and radius $$40\,cm.$$ What is the angular acceleration of the cylinder, if the rope is pulled with a force of $$30\,N$$ ?
A.
$$25\,m/{s^2}$$
B.
$$0.25\,rad/{s^2}$$
C.
$$25\,rad/{s^2}$$
D.
$$5\,m/{s^2}$$
Answer :
$$25\,rad/{s^2}$$
Solution :
Torque $$\left( \tau \right)$$ acting on a body and angular acceleration $$\left( \alpha \right)$$ produced in it are related as $$\tau = I\alpha $$
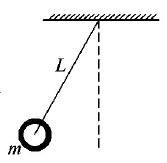
Consider a hollow cylinder, around which a rope is wounded as shown in the figure.

Torque acting on the cylinder due to the force $$F$$ is $$\tau = Fr$$
Now, we have $$\tau = I\alpha $$
where, $$I$$ = moment of inertia of the cylinder about the axis through the centre $$ = m{r^2}$$
$$\alpha $$ = angular acceleration
$$\eqalign{ & \Rightarrow \alpha = \frac{\tau }{I} = \frac{{Fr}}{{m{r^2}}} = \frac{F}{{mr}} = \frac{{30}}{{3 \times 40 \times {{10}^{ - 2}}}} \cr & = \frac{{100}}{4} = 25\,rad/{s^2} \cr} $$
Torque $$\left( \tau \right)$$ acting on a body and angular acceleration $$\left( \alpha \right)$$ produced in it are related as $$\tau = I\alpha $$
Consider a hollow cylinder, around which a rope is wounded as shown in the figure.

Torque acting on the cylinder due to the force $$F$$ is $$\tau = Fr$$
Now, we have $$\tau = I\alpha $$
where, $$I$$ = moment of inertia of the cylinder about the axis through the centre $$ = m{r^2}$$
$$\alpha $$ = angular acceleration
$$\eqalign{ & \Rightarrow \alpha = \frac{\tau }{I} = \frac{{Fr}}{{m{r^2}}} = \frac{F}{{mr}} = \frac{{30}}{{3 \times 40 \times {{10}^{ - 2}}}} \cr & = \frac{{100}}{4} = 25\,rad/{s^2} \cr} $$