Question
A resistance of $$2\Omega $$ is connected across one gap of a metrebridge (the length of the wire is $$100\,cm$$ ) and an unknown resistance, greater than $$2\Omega ,$$ is connected across the other gap. When these resistances are interchanged, the balance point shifts by $$20\,cm.$$ Neglecting any corrections, the unknown resistance is
A.
$$3\Omega $$
B.
$$4\Omega $$
C.
$$5\Omega $$
D.
$$6\Omega $$
Answer :
$$3\Omega $$
Solution :
Given $$X$$ is greater than $$2\Omega $$ when the bridge is balanced
$$\frac{R}{\ell } = \frac{X}{{100 - \ell }}$$
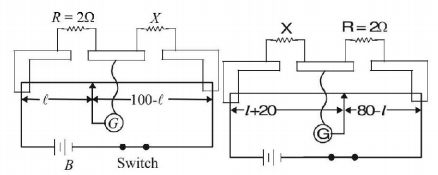
Case (i)
$$\eqalign{ & {\text{or,}}\,100R - R\ell = \ell X\,\,\,{\text{or,}}\,200 - 2\ell = \ell X \cr & {\text{or,}}\,\ell = \frac{{200}}{{X + 2}} \cr} $$
When the resistances are interchanged the jockey shifts $$20\,cm.$$ Therefore
$$\eqalign{ & \frac{X}{{\ell + 20}} = \frac{2}{{80 - \ell }} \cr & 80X - \ell X = 2\ell + 40 \cr & {\text{or,}}\,80X = \ell \left( {X + 2} \right) + 40 \cr & {\text{or,}}\,80X = \left( {\frac{{200}}{{X + 2}}} \right)\left( {X + 2} \right) + 40 \cr & {\text{or,}}\,X = \frac{{240}}{{80}} = 3\Omega . \cr} $$
Given $$X$$ is greater than $$2\Omega $$ when the bridge is balanced
$$\frac{R}{\ell } = \frac{X}{{100 - \ell }}$$

Case (i)
$$\eqalign{ & {\text{or,}}\,100R - R\ell = \ell X\,\,\,{\text{or,}}\,200 - 2\ell = \ell X \cr & {\text{or,}}\,\ell = \frac{{200}}{{X + 2}} \cr} $$
When the resistances are interchanged the jockey shifts $$20\,cm.$$ Therefore
$$\eqalign{ & \frac{X}{{\ell + 20}} = \frac{2}{{80 - \ell }} \cr & 80X - \ell X = 2\ell + 40 \cr & {\text{or,}}\,80X = \ell \left( {X + 2} \right) + 40 \cr & {\text{or,}}\,80X = \left( {\frac{{200}}{{X + 2}}} \right)\left( {X + 2} \right) + 40 \cr & {\text{or,}}\,X = \frac{{240}}{{80}} = 3\Omega . \cr} $$