Question
A rectangular glass slab $$ABCD$$ of refractive index $$n,$$ is immersed in water of refractive index $${n_2}\left( {{n_1} > {n_2}} \right).$$ A ray of light is incident at the surface $$AB$$ of the slab as shown. The maximum value of the angle of incidence $${\alpha _{\max }}$$ such that the ray comes out only from the other surface $$CD$$ is given by
A rectangular glass slab $$ABCD$$ of refractive index $$n,$$ is immersed in water of refractive index $${n_2}\left( {{n_1} > {n_2}} \right).$$ A ray of light is incident at the surface $$AB$$ of the slab as shown. The maximum value of the angle of incidence $${\alpha _{\max }}$$ such that the ray comes out only from the other surface $$CD$$ is given by

A.
$${\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right)} \right]$$
B.
$${\sin ^{ - 1}}\left[ {{n_1}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{1}{{{n_2}}}} \right)} \right)} \right]$$
C.
$${\sin ^{ - 1}}\left( {\frac{{{n_1}}}{{{n_2}}}} \right)$$
D.
$${\sin ^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)$$
Answer :
$${\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right)} \right]$$
Solution :
See figure. The ray will come out from $$CD$$ if it suffers total internal reflection at surface $$AD,$$ i.e., it strikes the surface $$AD$$ at critical angle $$C$$ ( the limiting case).
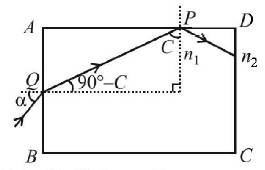
Applying Snell's law at $$P$$
$${n_1}\sin C = {n_2}\,{\text{or }}\sin C = \frac{{{n_2}}}{{{n_1}}}$$
Applying Snell's law at $$Q$$
$$\eqalign{ & {n_2}\sin \alpha = {n_1}\cos C \cr & \Rightarrow \,\,\sin \alpha = \frac{{{n_1}}}{{{n_2}}}\cos \left\{ {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right\} \cr & {\text{or }}\alpha = {\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left\{ {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right\}} \right] \cr} $$
See figure. The ray will come out from $$CD$$ if it suffers total internal reflection at surface $$AD,$$ i.e., it strikes the surface $$AD$$ at critical angle $$C$$ ( the limiting case).

Applying Snell's law at $$P$$
$${n_1}\sin C = {n_2}\,{\text{or }}\sin C = \frac{{{n_2}}}{{{n_1}}}$$
Applying Snell's law at $$Q$$
$$\eqalign{ & {n_2}\sin \alpha = {n_1}\cos C \cr & \Rightarrow \,\,\sin \alpha = \frac{{{n_1}}}{{{n_2}}}\cos \left\{ {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right\} \cr & {\text{or }}\alpha = {\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left\{ {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right\}} \right] \cr} $$