Question
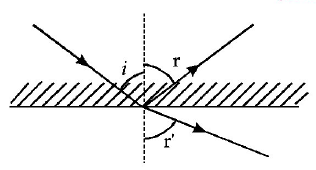
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
A.
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
B.
$${\sin ^{ - 1}}\left( {\tan i} \right)$$
C.
$${\sin ^{ - 1}}\left( {\tan r'} \right)$$
D.
$${\tan ^{ - 1}}\left( {\sin i} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
Solution :
$$C = {\sin ^{ - 1}}\left( {\frac{1}{{_2^1\mu }}} \right)\,\,\,.....\left( {\text{i}} \right)$$
Applying Snell's law at $$P,$$ we get
$$\eqalign{ & _2^1\mu = \frac{{\sin r'}}{{\sin i}} \cr & = \frac{{\sin \left( {90 - r} \right)}}{{\sin r}}\left[ {\because \,\,i = r,r' + r = {{90}^ \circ }} \right] \cr & \because \,\,_2^1\mu = \frac{{\cos r}}{{\sin r}}\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii)
$$C = {\sin ^{ - 1}}\left( {\tan r} \right)$$
$$C = {\sin ^{ - 1}}\left( {\frac{1}{{_2^1\mu }}} \right)\,\,\,.....\left( {\text{i}} \right)$$
Applying Snell's law at $$P,$$ we get
$$\eqalign{ & _2^1\mu = \frac{{\sin r'}}{{\sin i}} \cr & = \frac{{\sin \left( {90 - r} \right)}}{{\sin r}}\left[ {\because \,\,i = r,r' + r = {{90}^ \circ }} \right] \cr & \because \,\,_2^1\mu = \frac{{\cos r}}{{\sin r}}\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii)
$$C = {\sin ^{ - 1}}\left( {\tan r} \right)$$