Question
A ray is incident at an angle of incidence $$i$$ on one surface of a prism of small angle $$A$$ and emerge normally from opposite surface. If the refractive index of the material of prism is $$\mu ,$$ the angle of incidence $$i$$ is nearly equal to
A.
$$\frac{A}{\mu }$$
B.
$$\frac{A}{{2\mu }}$$
C.
$$\mu A$$
D.
$$\frac{{\mu A}}{2}$$
Answer :
$$\mu A$$
Solution :
Angle of prism is given by $$A = {r_1} + {r_2}$$
where, $${r_1}$$ is refraction angle on incident face and $${r_2}$$ is angle of incidence on 2nd face of prism. As refracted ray emerges normally from opposite surface, $${r_2} = 0.$$
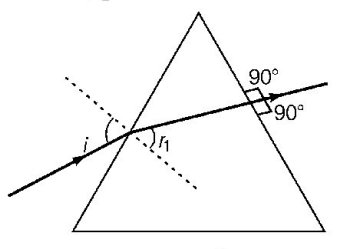
$$\eqalign{ & \therefore A = {r_1} \cr & {\text{Now,}}\,\,\mu = \frac{{\sin i}}{{\sin {r_1}}} \cr} $$
If $$\angle {i_1}$$ and $$\angle {r_1}$$ are very small then, $$\sin i \approx i,\sin {r_1} \approx {r_1}$$
$$\eqalign{ & \therefore \mu = \frac{i}{{{r_1}}} = \frac{i}{A} \cr & \therefore i = \mu A \cr} $$
Angle of prism is given by $$A = {r_1} + {r_2}$$
where, $${r_1}$$ is refraction angle on incident face and $${r_2}$$ is angle of incidence on 2nd face of prism. As refracted ray emerges normally from opposite surface, $${r_2} = 0.$$

$$\eqalign{ & \therefore A = {r_1} \cr & {\text{Now,}}\,\,\mu = \frac{{\sin i}}{{\sin {r_1}}} \cr} $$
If $$\angle {i_1}$$ and $$\angle {r_1}$$ are very small then, $$\sin i \approx i,\sin {r_1} \approx {r_1}$$
$$\eqalign{ & \therefore \mu = \frac{i}{{{r_1}}} = \frac{i}{A} \cr & \therefore i = \mu A \cr} $$