Question
A projectile is thrown in the upward direction making an angle of $${60^ \circ }$$ with the horizontal direction with a velocity of $$147\,m{s^{ - 1}}.$$ Then the time after which its inclination with the horizontal is $${45^ \circ },$$ is
A.
$$15\,s$$
B.
$$10.98\,s$$
C.
$$5.49\,s$$
D.
$$2.745\,s$$
Answer :
$$5.49\,s$$
Solution :
Velocity of projectile $$u = 147\,m{s^{ - 1}}$$
angle of projection $$\alpha = {60^ \circ }$$
Let, the time taken by the Projectile from $$O$$ to $$A$$ be $$t$$ where direction $$\beta = {45^ \circ }.$$ As horizontal component of velocity remains constant during the projectile motion.
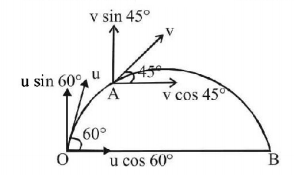
$$\eqalign{ & \Rightarrow v\cos {45^ \circ } = u\cos {60^ \circ } \cr & \Rightarrow v \times \frac{1}{{\sqrt 2 }} = 147 \times \frac{1}{2}\, \Rightarrow v = \frac{{147}}{{\sqrt 2 }}m{s^{ - 1}} \cr} $$
For Vertical motion,
$$\eqalign{ & {v_y} = {u_y} - gt \cr & \Rightarrow v\sin {45^ \circ } = 45\sin {60^ \circ } - 9.8t \cr & \Rightarrow \frac{{147}}{{\sqrt 2 }} \times \frac{1}{{\sqrt 2 }} = 147 \times \frac{{\sqrt 3 }}{2} - 9.8t \cr & \Rightarrow 9.8t = \frac{{147}}{2}\left( {\sqrt 3 - 1} \right) \Rightarrow t = 5.49\,s \cr} $$
Velocity of projectile $$u = 147\,m{s^{ - 1}}$$
angle of projection $$\alpha = {60^ \circ }$$
Let, the time taken by the Projectile from $$O$$ to $$A$$ be $$t$$ where direction $$\beta = {45^ \circ }.$$ As horizontal component of velocity remains constant during the projectile motion.

$$\eqalign{ & \Rightarrow v\cos {45^ \circ } = u\cos {60^ \circ } \cr & \Rightarrow v \times \frac{1}{{\sqrt 2 }} = 147 \times \frac{1}{2}\, \Rightarrow v = \frac{{147}}{{\sqrt 2 }}m{s^{ - 1}} \cr} $$
For Vertical motion,
$$\eqalign{ & {v_y} = {u_y} - gt \cr & \Rightarrow v\sin {45^ \circ } = 45\sin {60^ \circ } - 9.8t \cr & \Rightarrow \frac{{147}}{{\sqrt 2 }} \times \frac{1}{{\sqrt 2 }} = 147 \times \frac{{\sqrt 3 }}{2} - 9.8t \cr & \Rightarrow 9.8t = \frac{{147}}{2}\left( {\sqrt 3 - 1} \right) \Rightarrow t = 5.49\,s \cr} $$