Question
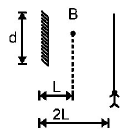
A point source of light $$B$$ is placed at a distance $$L$$ in front of the centre of a mirror of width $$'d’$$ hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance $$2\,L$$ from it as shown in fig. The greatest distance over which he can see the image of the light source in the mirror is
A point source of light $$B$$ is placed at a distance $$L$$ in front of the centre of a mirror of width $$'d’$$ hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance $$2\,L$$ from it as shown in fig. The greatest distance over which he can see the image of the light source in the mirror is
A.
$$\frac{d}{2}$$
B.
$$d$$
C.
$$2\,d$$
D.
$$3\,d$$
Answer :
$$3\,d$$
Solution :
From the ray diagram.

$$\eqalign{ & {\text{In }}\Delta \,ANM\,\,{\text{and }}\Delta \,ADB \cr & \angle \,ADB = \angle \,ANM = {90^ \circ } \cr & \angle \,MAN = \angle \,BAN\,\,\left( {{\text{laws of reflection}}} \right) \cr & {\text{Also, }}\angle \,BAN = \angle \,ABD \cr & \Rightarrow \,\,\angle \,MAN = \angle \,ABD \cr} $$
∴ $$\Delta \,ANM$$ is similar to $$\Delta \,ADB$$
$$\therefore \,\,\frac{x}{{2\,L}} = \frac{{\frac{d}{2}}}{L}\,\,{\text{or }}x = d$$
So, required distance $$= d + d + d = 3\,d.$$
From the ray diagram.

$$\eqalign{ & {\text{In }}\Delta \,ANM\,\,{\text{and }}\Delta \,ADB \cr & \angle \,ADB = \angle \,ANM = {90^ \circ } \cr & \angle \,MAN = \angle \,BAN\,\,\left( {{\text{laws of reflection}}} \right) \cr & {\text{Also, }}\angle \,BAN = \angle \,ABD \cr & \Rightarrow \,\,\angle \,MAN = \angle \,ABD \cr} $$
∴ $$\Delta \,ANM$$ is similar to $$\Delta \,ADB$$
$$\therefore \,\,\frac{x}{{2\,L}} = \frac{{\frac{d}{2}}}{L}\,\,{\text{or }}x = d$$
So, required distance $$= d + d + d = 3\,d.$$