Question
A piece of wire is bent in the shape of a parabola $$y = k{x^2}$$ ($$y$$-axis vertical) with a bead of mass $$m$$ on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the $$x$$-axis with a constant acceleration $$a.$$ The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the $$y$$-axis is-
A.
$$\frac{a}{{gk}}$$
B.
$$\frac{a}{{2gk}}$$
C.
$$\frac{{2a}}{{gk}}$$
D.
$$\frac{a}{{4gk}}$$
Answer :
$$\frac{a}{{2gk}}$$
Solution :
The forces acting on the bead as seen by the observer in the accelerated frame are : (a) $$N ;$$ (b) $$mg ;$$ (c) $$ma$$ (pseudo force).
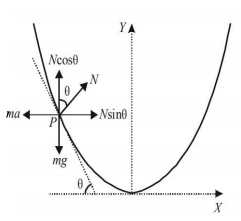
Let $$\theta $$ is the angle which the tangent at $$P$$ makes with the X- axis. As the bead is in equilibrium with respect to the wire, therefore $$N\sin \theta = ma\,\,{\text{and }}N\cos \theta = mg$$
$$\therefore \tan \theta = \frac{a}{g}.....(i)$$
But $$y = k{x^2}$$
Therefore,
$$\frac{{dy}}{{dx}} = 2kx = \tan \theta .....(ii)$$
From $$(i)\,\& \,(ii)$$
$$2kx = \frac{a}{g}\,\,\,\, \Rightarrow x = \frac{a}{{2kg}}$$
The forces acting on the bead as seen by the observer in the accelerated frame are : (a) $$N ;$$ (b) $$mg ;$$ (c) $$ma$$ (pseudo force).

Let $$\theta $$ is the angle which the tangent at $$P$$ makes with the X- axis. As the bead is in equilibrium with respect to the wire, therefore $$N\sin \theta = ma\,\,{\text{and }}N\cos \theta = mg$$
$$\therefore \tan \theta = \frac{a}{g}.....(i)$$
But $$y = k{x^2}$$
Therefore,
$$\frac{{dy}}{{dx}} = 2kx = \tan \theta .....(ii)$$
From $$(i)\,\& \,(ii)$$
$$2kx = \frac{a}{g}\,\,\,\, \Rightarrow x = \frac{a}{{2kg}}$$