Question
A particle starting from the origin $$\left( {0,0} \right)$$ moves in a straight line in the $$\left( {x,y} \right)$$ plane. Its co-ordinates at a later time are $$\left( {\sqrt 3 ,3} \right).$$ The path of the particle makes with the $$x$$-axis an angle of
A.
$${30^ \circ }$$
B.
$${45^ \circ }$$
C.
$${60^ \circ }$$
D.
$${0^ \circ }$$
Answer :
$${60^ \circ }$$
Solution :
Draw the situation as given in questions. $$OA$$ represents the path of the particle starting from origin $$O\left( {0,0} \right).$$ Draw a perpendicular from point $$A$$ to $$x$$-axis. Let path of the particle makes an angle $$\theta $$ with the $$x$$-axis, then
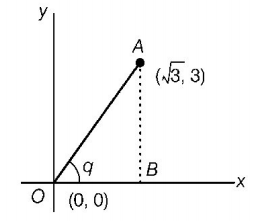
$$\eqalign{ & \tan \theta = {\text{slope of line }}OA \cr & \,\,\,\,\,\,\,\,\,\,\, = {\text{path of the particle }}1{\text{ making angle }}\theta \cr & \tan \theta = \frac{{3 - 0}}{{\sqrt 3 - 0}} = \sqrt 3 \cr & \,\,\,\,\,\,\theta = {60^ \circ } \cr} $$
Draw the situation as given in questions. $$OA$$ represents the path of the particle starting from origin $$O\left( {0,0} \right).$$ Draw a perpendicular from point $$A$$ to $$x$$-axis. Let path of the particle makes an angle $$\theta $$ with the $$x$$-axis, then

$$\eqalign{ & \tan \theta = {\text{slope of line }}OA \cr & \,\,\,\,\,\,\,\,\,\,\, = {\text{path of the particle }}1{\text{ making angle }}\theta \cr & \tan \theta = \frac{{3 - 0}}{{\sqrt 3 - 0}} = \sqrt 3 \cr & \,\,\,\,\,\,\theta = {60^ \circ } \cr} $$