Releted MCQ Question on
Basic Physics >> Uniform Circular Motion
Releted Question 1
A small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
A.


B.


C.
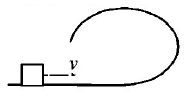

D.


Releted Question 2
A block $$P$$ of mass $$m$$ is placed on a horizontal frictionless plane. A second block of same mass $$m$$ is placed on it and is connected to a spring of spring constant $$k,$$ the two blocks are pulled by distance $$A.$$ Block $$Q$$ oscillates without slipping. What is the maximum value of frictional force between the two blocks.
A block $$P$$ of mass $$m$$ is placed on a horizontal frictionless plane. A second block of same mass $$m$$ is placed on it and is connected to a spring of spring constant $$k,$$ the two blocks are pulled by distance $$A.$$ Block $$Q$$ oscillates without slipping. What is the maximum value of frictional force between the two blocks.

A.
$$\frac{{kA}}{2}$$
B.
$$kA$$
C.
$${\mu _s}mg$$
D.
zero
Releted Question 3
A ball of mass $$\left( m \right) 0.5kg$$ is attached to the end of a string having length $$\left( L \right)\,0.5m.$$ The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is $$324N.$$ The maximum possible value of angular velocity of ball (in radian/s) is
A ball of mass $$\left( m \right) 0.5kg$$ is attached to the end of a string having length $$\left( L \right)\,0.5m.$$ The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is $$324N.$$ The maximum possible value of angular velocity of ball (in radian/s) is
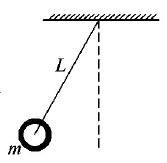
A.
9
B.
18
C.
27
D.
36
Releted Question 4
An annular ring with inner and outer radii $${R_1}$$ and $${R_2}$$ is rolling without slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, $$\frac{{{F_1}}}{{{F_2}}}$$ is
A.
$${\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^2}$$
B.
$$\frac{{{R_2}}}{{{R_1}}}$$
C.
$$\frac{{{R_1}}}{{{R_2}}}$$
D.
1