Question
A particle of mass $$m$$ oscillates with simple harmonic motion between points $${x_1}$$ and $${x_2},$$ the equilibrium position being $$O.$$ Its potential energy is plotted. It will be as given below in the graph
A.
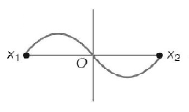

B.
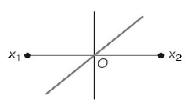

C.
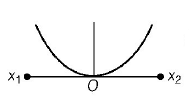

D.
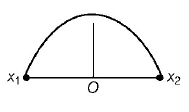

Answer :


Solution :
Potential energy is given by $$U = \frac{1}{2}k{x^2}$$
The corresponding graph is shown in figure.
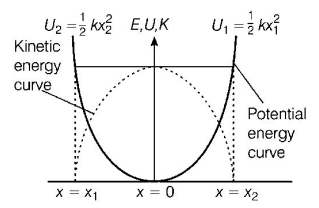
At equilibrium position $$\left( {x = 0} \right),$$ potential energy is minimum. At extreme positions $${x_1}$$ and $${x_2},$$ its potential energies are
$${U_1} = \frac{1}{2}kx_1^2\,\,{\text{and}}\,\,{U_2} = \frac{1}{2}kx_2^2$$
NOTE
In the above graph, the dotted line (curve) is shown for kinetic energy. This graph shows that kinetic energy is maximum at mean position and zero at extreme positions $${x_1}$$ and $${x_2}.$$
Potential energy is given by $$U = \frac{1}{2}k{x^2}$$
The corresponding graph is shown in figure.

At equilibrium position $$\left( {x = 0} \right),$$ potential energy is minimum. At extreme positions $${x_1}$$ and $${x_2},$$ its potential energies are
$${U_1} = \frac{1}{2}kx_1^2\,\,{\text{and}}\,\,{U_2} = \frac{1}{2}kx_2^2$$
NOTE
In the above graph, the dotted line (curve) is shown for kinetic energy. This graph shows that kinetic energy is maximum at mean position and zero at extreme positions $${x_1}$$ and $${x_2}.$$