Question
A particle of mass $$m$$ moving in the $$x$$ direction with speed $$2v$$ is hit by another particle of mass $$2m$$ moving in the $$y$$ direction with speed $$v.$$ If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
A.
56%
B.
62%
C.
44%
D.
50%
Answer :
56%
Solution :
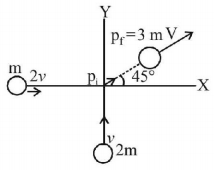
Initial momentum of the system
$$\eqalign{ & {p_{net}} = \sqrt {{{\left\{ {\left( {2m} \right)v} \right\}}^2} + {{\left\{ {m\left( {2v} \right)} \right\}}^2}} \cr & {p_{net}} = \sqrt {4{m^2}{v^2} + 4{m^2}{v^2}} \cr & {p_{net}} = \sqrt {8{m^2}{v^2}} \cr & {p_{net}} = 2\sqrt 2 mv \cr} $$
Final momentum of the system $$= 3mV$$
By the law of conservation of momentum
$$\eqalign{ & {p_{net}} = 3m{V_{combined}} \cr & \Rightarrow 2\sqrt 2 mv = 3m{V_{combined}} \cr & \Rightarrow \frac{{2\sqrt 2 v}}{3} = {V_{combined}} \cr} $$
Loss in energy
$$\eqalign{ & \Delta E = \frac{1}{2}{m_1}V_1^2 + \frac{1}{2}{m_2}V_2^2 - \frac{1}{2}\left( {{m_1} + {m_2}} \right)V_{combined}^2 \cr & DE = 3m{v^2} - \frac{4}{3}m{v^2} = \frac{5}{3}m{v^2} = 55.55\% \cr} $$
Percentage loss in energy during the collision $$= 56\%$$

Initial momentum of the system
$$\eqalign{ & {p_{net}} = \sqrt {{{\left\{ {\left( {2m} \right)v} \right\}}^2} + {{\left\{ {m\left( {2v} \right)} \right\}}^2}} \cr & {p_{net}} = \sqrt {4{m^2}{v^2} + 4{m^2}{v^2}} \cr & {p_{net}} = \sqrt {8{m^2}{v^2}} \cr & {p_{net}} = 2\sqrt 2 mv \cr} $$
Final momentum of the system $$= 3mV$$
By the law of conservation of momentum
$$\eqalign{ & {p_{net}} = 3m{V_{combined}} \cr & \Rightarrow 2\sqrt 2 mv = 3m{V_{combined}} \cr & \Rightarrow \frac{{2\sqrt 2 v}}{3} = {V_{combined}} \cr} $$
Loss in energy
$$\eqalign{ & \Delta E = \frac{1}{2}{m_1}V_1^2 + \frac{1}{2}{m_2}V_2^2 - \frac{1}{2}\left( {{m_1} + {m_2}} \right)V_{combined}^2 \cr & DE = 3m{v^2} - \frac{4}{3}m{v^2} = \frac{5}{3}m{v^2} = 55.55\% \cr} $$
Percentage loss in energy during the collision $$= 56\%$$